Question

【题目】（1）（观察发现）如图 1，△ABC 和△CDE 都是等边三角形，且点 B、C、E 在一条直线上，连接 BD 和AE，BD、AE 相交于点 P，则线段 BD 与 AE 的数量关系是 ，BD 与 AE 相交构成的锐角的度数是 .（只要求写出结论，不必说明理由）

（2）（深入探究 1）如图 2，△ABC 和△CDE 都是等边三角形，连接 BD 和 AE，BD、AE 相交于点 P，猜想线段 BD 与 AE 的数量关系，以及 BD 与 AE 相交构成的锐角的度数. 请说明理由 结论：

理由：_______________________

（3）（深入探究 2）如图 3，△ABC 和△CDE 都是等腰直角三角形，且∠ACB＝∠DCE＝90°，连接 AD、BE，Q 为 AD 中点，连接 QC 并延长交 BE 于 K. 求证：QK⊥BE.

Answer 1

【答案】（1）BD=AE，60°；

（2）BD=AE，60°；

（3）证明见详解.

【解析】

（1）根据等边三角形的性质可得AB=AC，CD=CE，∠ACB=∠DCE=60°，然后求出∠ACE=∠BCD，再利用“边角边”证明△ACE和△BCD全等，根据全等三角形对应边相等可得BD=AE，根据全等三角形对应角相等可得∠AEC=∠BDC，然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠DPE=∠DCE；
（2）根据等边三角形的性质可得AB=AC，CD=CE，∠ACB=∠DCE=60°，然后求出∠ACE=∠BCD，再利用“边角边”证明△ACE和△BCD全等，根据全等三角形对应边相等可得BD=AE，根据全等三角形对应角相等可得∠AEC=∠BDC，然后根据三角形的内角和定理求出∠DPE=∠DEC；

（3）延长CQ到R，使得CQ=QR，连接AR、DR．只要证明△ACR≌△BCE，可得∠ACR=∠CBE，由∠ACR+∠BCK=90°，推出∠CBE+∠BCK=90°，可得∠CKB=90°，即CK⊥BE．

解：（1）∵△ABC和△CDE都是等边三角形，
∴AB=AC，CD=CE，∠ACB=∠DCE=60°，
∴∠ACB+∠ACD=∠DCE+∠ACD，
即∠ACE=∠BCD，
在△ACE和△BCD中，

，

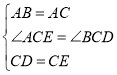∴△ACE≌△BCD（SAS），
∴BD=AE，∠AEC=∠BDC，
由三角形的外角性质，∠DPE=∠AEC+∠DBC，
∠DCE=∠BDC+∠DBC，
∴∠DPE=∠DCE=60°；

（2）结论BD=AE，∠DPE=60°还成立．
∵△ABC和△CDE都是等边三角形，
∴AB=AC，CD=CE，∠ACB=∠DCE=60°，
∴∠ACB+∠ACD=∠DCE+∠ACD，
即∠ACE=∠BCD，
在△ACE和△BCD中，

，

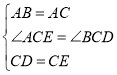∴△ACE≌△BCD（SAS），
∴BD=AE，∠AEC=∠BDC，
∵∠BDC+∠CDE+∠AED

=∠AEC+∠CDE+∠AED

=∠CDE+∠CED

=180°-∠DCE

=180°-60°=120°，
∴∠DPE=180°-（∠BDC+∠CDE+∠AED）=180°-120°=60°；

（3）如图3中，延长CQ到F，使得CQ=QF，连接AF、DF．

∵△ABC和△CDE都是等腰直角三角形，
∴∠ACB=∠DCE=90°，AC=BC，CE=CD，
∴∠BCE+∠ACD=180°，
∵Q 为 AD 中点,

∴AQ=DQ，

∵CQ=QF，
∴四边形ACDF是平行四边形，
∴AF=CD=CE，AF∥CD，
∴∠CAF+∠ACD=180°，
∴∠BCE=∠CAF，∵CA=CB，AF=CE，
∴△ACF≌△BCE，
∴∠ACF=∠CBE，
∵∠ACF+∠BCK=180°-∠ACB =180°-90°=90°，
∴∠CBE+∠BCK=90°，
∴∠CKB=90°，即CK⊥BE．