题目内容
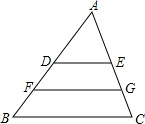如图，△ABC中，D、E分别为AB、AC的中点，F、G分别为DB、EC的中点，若BC=4cm，则FG=________cm．
3
分析：根据三角形的中位线平行于第三边并且等于第三边的一半求出DE的长度，再根据梯形的中位线等于两底和的一半列式计算即可得解．
解答：∵D、E分别为AB、AC的中点，
∴DE是△ABC的中位线，
∵BC=4cm，
∴DE=
BC=×4=2cm，
∵F、G分别为DB、EC的中点，
∴FG是梯形DBCE的中位线，
∴FG=（DE+BC）=（2+4）=3cm．
故答案为：3．
点评：本题考查了三角形的中位线定理，梯形的中位线定理，熟记定理是解题的关键，要注意这两个定理都是两个结论．
分析：根据三角形的中位线平行于第三边并且等于第三边的一半求出DE的长度，再根据梯形的中位线等于两底和的一半列式计算即可得解．
解答：∵D、E分别为AB、AC的中点，
∴DE是△ABC的中位线，
∵BC=4cm，
∴DE=
BC=×4=2cm，∵F、G分别为DB、EC的中点，
∴FG是梯形DBCE的中位线，
∴FG=
（DE+BC）=（2+4）=3cm．故答案为：3．
点评：本题考查了三角形的中位线定理，梯形的中位线定理，熟记定理是解题的关键，要注意这两个定理都是两个结论．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
26、已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．
27、已知：如图，△ABC中，∠BAC=60°，D、E两点在直线BC上，连接AD、AE．
27、如图，△ABC中，AD⊥BC于D，DN⊥AC于N，DM⊥AB于M
14、如图，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
已知，如图，△ABC中，点D在BC上，且∠1=∠C，∠2=2∠3，∠BAC=70°．