题目内容
(2011•泉州质检)已知:如图,等边△ABC和正方形ACPQ的边长都是1,在图形所在的平面内,以点A为旋转中心 将正方形ACPQ沿逆时针方向旋转α,使AQ与AB重合,则:
将正方形ACPQ沿逆时针方向旋转α,使AQ与AB重合,则:
(1)旋转角α=
(2)点P从开始到结束所经过的路线长为
π
π.
 将正方形ACPQ沿逆时针方向旋转α,使AQ与AB重合,则:
将正方形ACPQ沿逆时针方向旋转α,使AQ与AB重合,则:(1)旋转角α=
210
210
°;(2)点P从开始到结束所经过的路线长为
7
| ||
| 6 |
7
| ||
| 6 |
分析:(1)根据△ABC是等边三角形,ACPQ是正方形,得出∠BAC=60°,∠CAQ=90°,求出∠BAQ的度数即可求出旋转角α;
(2)连接AP,得出AP的长,根据旋转角和弧长公式即可求出点P从开始到结束所经过的路线长;
(2)连接AP,得出AP的长,根据旋转角和弧长公式即可求出点P从开始到结束所经过的路线长;
解答: 解:(1)∵∠BAC=60°,∠CAQ=90°,
解:(1)∵∠BAC=60°,∠CAQ=90°,
∴∠α=∠BAQ=360°-60°-90°=210°,
∴旋转角α=210°,
(2)连接AP,
∵AP=
=
,
∴点P从开始到结束所经过的路线长为=
=
π;
故填:210°,
π.
 解:(1)∵∠BAC=60°,∠CAQ=90°,
解:(1)∵∠BAC=60°,∠CAQ=90°,∴∠α=∠BAQ=360°-60°-90°=210°,
∴旋转角α=210°,
(2)连接AP,
∵AP=
| AC2+PC2 |
| 2 |
∴点P从开始到结束所经过的路线长为=
210•π×
| ||
| 180 |
7
| ||
| 6 |
故填:210°,
7
| ||
| 6 |
点评:此题考查了旋转的性质;关键是作出辅助线,列出求路线长的式子.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
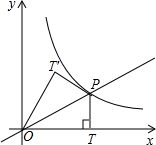 (2011•泉州质检)如图,点P(m,1)是双曲线y=
(2011•泉州质检)如图,点P(m,1)是双曲线y= 用“>、<、=、≥、≤”符号表示);
用“>、<、=、≥、≤”符号表示);