题目内容
19.已知a1=$\frac{1}{t}$,a2=$\frac{1}{1-{a}_{1}}$,a3=$\frac{1}{1-{a}_{2}}$,…,an+1=$\frac{1}{1-{a}_{n}}$,(n为正整数,且t≠0,1),则a50=$\frac{t}{t-1}$(用含t的代数式表示)分析 分别根据运算规则求出前4个数,继而可得数列每3个数为一个周期循环,从而得出答案.
解答 解:∵a1=$\frac{1}{t}$,
∴a2=$\frac{1}{1-\frac{1}{t}}$=$\frac{t}{t-1}$,
a3=$\frac{1}{1-\frac{t}{t-1}}$=1-t,
a4=$\frac{1}{1-(1-t)}$=$\frac{1}{t}$,
…
∴以上数列每3个数为一个周期循环,
∵50÷3=16…2,
∴a50=a2=$\frac{t}{t-1}$,
故答案为:$\frac{t}{t-1}$.
点评 本题主要考查数字的变化规律,根据题意得出数列每3个数为一个周期循环是解题的关键.

练习册系列答案
相关题目
10.下列根式属于最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{6}$ | C. | $\sqrt{1.5}$ | D. | $\sqrt{\frac{1}{2}}$ |
14.下列算式中,结果是x6的是( )
| A. | x3•x2 | B. | x12÷x2 | C. | (x2)3 | D. | 2x6+3x6 |

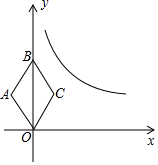 如图,在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$(x>0)的图象和菱形OABC,且OB=4,tan∠BOC=$\frac{1}{2}$.
如图,在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$(x>0)的图象和菱形OABC,且OB=4,tan∠BOC=$\frac{1}{2}$.
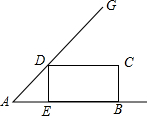 如图,∠A=45°,AB=30,点E在线段AB上运动,过点E作DE⊥AB,交AG于点D.以DE、EB为邻边作矩形BCDE.将△ADE沿直线DE翻折,使点A落在点F处.设矩形BCDE与△ADF重叠部分的面积为S,线段DE的长为x(0<x<30).
如图,∠A=45°,AB=30,点E在线段AB上运动,过点E作DE⊥AB,交AG于点D.以DE、EB为邻边作矩形BCDE.将△ADE沿直线DE翻折,使点A落在点F处.设矩形BCDE与△ADF重叠部分的面积为S,线段DE的长为x(0<x<30). 如图,在平面直角坐标系中,点A的坐标为(0,$\frac{29}{2}$),直线y=-$\frac{5}{12}$x-5与x轴、y轴分别交于B、C,点P是直线BC上的一个动点,则AP长的最小值为18.
如图,在平面直角坐标系中,点A的坐标为(0,$\frac{29}{2}$),直线y=-$\frac{5}{12}$x-5与x轴、y轴分别交于B、C,点P是直线BC上的一个动点,则AP长的最小值为18.