题目内容
如图,△OAC和△ADB都是等腰直角三角形,∠ACO=∠ADB=90°,点D在线段AC上,反比例函数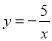 经过点B,则
经过点B,则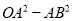 等于 ( )
等于 ( )

A. 5 B. 10 C. 15 D. 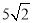
练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
题目内容
如图,△OAC和△ADB都是等腰直角三角形,∠ACO=∠ADB=90°,点D在线段AC上,反比例函数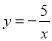 经过点B,则
经过点B,则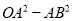 等于 ( )
等于 ( )

A. 5 B. 10 C. 15 D. 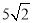
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案