��Ŀ����
����Ŀ����������һ����30���ǵ�ֱ�������η���һ������ֽƬ�ϣ�
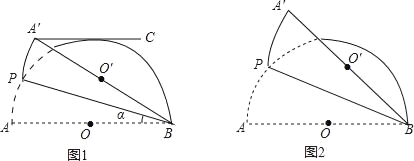
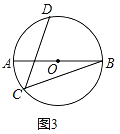
��1����ͼ1��ʾ��ֱ�Ƕ���P�ڳ����εı�AB�ϣ�ֱ�DZ߽������ε�����AD��BC�ڵ�E��F�����ͼ�еġ�1=140������ô��2= �ȣ�
��2����ͼ2��ʾ��ֱ�Ƕ���P�ڳ������ڣ��ҳ����εĶ���A��B�ڡ�P��ֱ�DZ��ϣ���ôͼ�еġ�1���2���������Ĺ�ϵ��Ϊʲô��
��3�������30������ͼ3�ڷţ�ʹ�ó����εĶ���A��B��30���ǵ������ϣ���ʱ������Ϊͼ�еġ�1���2���������Ĺ�ϵ����ֱ��д����Ľ��ۣ� .
���𰸡�130�㣻���ࣻ��2=��1+30��
��������
���⿼�����ƽ���ߵ����ʺͳ����ε������Լ�������ڽǺͣ����ö�����ڽǺ�������ƽ��ͬ���ڽǻ������ɽ��ڣ�1����������ֱ��ƽ�У�ͬ���ڽǻ��������ͼ�μ��������2����������ֱ��ƽ�У��ڴ�����ȼ��������3��
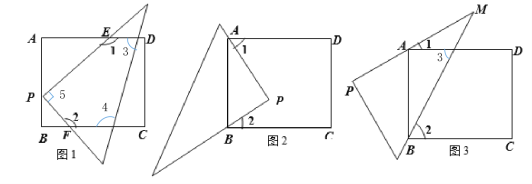
��1����ͼ1����Ϊ��1+��2+��3+��4+��5=540�㣨������ڽǺͶ���������3+��4=180�㣨��ֱ��ƽ��ͬ���ڽǻ���������5=90�㣬���ԡ�1+��2=270�㣬��Ϊ��1=140�㣬���ԡ�2=130�㣻
��2����ΪAD��BC�����ԡ�DAB+��CBA=180�㣬��Ϊ��P=90�㣬���ԡ�PAB+��PBA=90�㣬���ԡ�1+��2=����DAB+��CBA��-����PAB+��PBA��=90�㣬����1���2���ࣻ
��3����ΪAD��BC�����ԡ�2=��3����Ϊ��3=��1+��M������3=��1+30�㣬���ԡ�2=��1+30��

 ��������ϵ�д�
��������ϵ�д�