题目内容
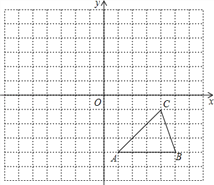
【题目】如图，在直角三角形
中，
，
．点
是直线
上一个动点(点不与点
，
重合)，连接
，在线段
的延长线上取一点
，使得
．过点
作
，交直线
于点
．
（1）如图1，当点在线段上时，若
，则
_________；
（2）当点在线段
的延长线上时，在图2中依题意补全图形，并判断
与
有怎样的数量关系，写出你的结论，并证明；
（3）在点运动的过程中，直接写出与的数量关系为_________．
【答案】（1）
；（2）图见解析，
，证明见解析；（3）当点P在线段AC与CA的延长线上时，当点P在AC的延长线上时
【解析】
（1）根据三角形的内角和定理及外角的性质进行角度的计算即可得解；
（2）根据三角形的内角和定理及外角的性质进行角度的计算即可得解；
（3）通过分类讨论，结合（1）（2）根据三角形的内角和定理及外角的性质进行角度的计算即可得解.
（1）解：∵
∴
∵
∴
∴
∵
∴
∴
；
（2）如下图所示：
证明：∵
∴
∵
∴
∴
∵
∴
又∵
∴
∵
∴；
（3）由（1）（2）可知，当点P在线段AC与CA的延长线上时，
当点P在AC的延长线上时，如下图所示：
设
∴
∵
∴
∵，
∴
∴
，
∴
则当点P在线段AC与CA的延长线上时，当点P在AC的延长线上时.
练习册系列答案
相关题目
