题目内容
若三角形a、b、c满足a2+b2+c2-10a-6b-8c+50=0,则此三角形为( )
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
考点:因式分解的应用
专题:
分析:利用一次项的系数分别求出常数项,把50分成9、16、25,然后与(a2-6a)、(b2-8b)、(c2-10c)分别组成完全平方公式,再利用非负数的性质,可分别求出a、b、c的值,然后利用勾股定理逆定理可证△ABC为直角三角形.
解答:解:∵a2+b2+c2-6a-8b-10c+50=0,
∴a2-6a+9+b2-8b+16+c2-10c+25=0,
即(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5,
∵32+42=52,
∴△ABC是直角三角形.
故选:C.
∴a2-6a+9+b2-8b+16+c2-10c+25=0,
即(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5,
∵32+42=52,
∴△ABC是直角三角形.
故选:C.
点评:本题考查了因式分解的应用、勾股定理逆定理、非负数的性质,解题的关键是注意配方法的步骤,在变形的过程中不要改变式子的值.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
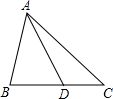 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )| A、AB2=BD•BC |
| B、AB2=BD•AC |
| C、AB•AD=BD•BC |
| D、AD•BC=BD•AC |
把方程-2x2-4x+1=0化为(x+h)2+k=0的形式,正确的是( )
| A、-(x+1)2-1=0 | ||
| B、(x-1)2-1=0 | ||
C、(x+1)2-
| ||
D、(2x+1)2-
|
分式
,
,
,
中最简分式有( )
| a |
| x |
| x+y |
| x2-y2 |
| 2a-b |
| 4a2-4ab+b2 |
| x+y |
| x-y |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列约分正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
把2x2-4x分解因式,结果正确的是( )
| A、(x+2)(x-2) |
| B、2x(x-2) |
| C、2(x2-2x) |
| D、x(2x-4) |
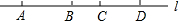 已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|=-(6-n)2.
已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|=-(6-n)2. 已知线段AB如图.
已知线段AB如图.