题目内容

平面直角坐标系内，点A（n，1-n）一定不在（ ）
A．第一象限
B．第二象限
C．第三象限
D．第四象限
【答案】分析：本题可转化为解不等式组的问题，求出无解的不等式即可．
解答：解：法1：由题意可得、、、，
解这四组不等式可知无解，
因而点A的横坐标是负数，纵坐标是负数，不能同时成立，即点A一定不在第三象限．
法2：点A横纵坐标满足x+y=1，即点A（n，1-n）在直线y=1-x上，
而y=1-x过一、二、四象限，
故A（n，1-n）一定不在第三象限．
故选C．
点评：本题主要考查平面直角坐标系中各象限内点的坐标的符号，把符号问题转化为解不等式组的问题．
练习册系列答案
相关题目
我们给出如下定义：如图①，平面内两条直线l1、l2相交于点O，对于平面内的任意一点M，若p、q分别是点M到直线l1和l2的距离（P≥0，q≥0），称有序非负实数对[p，q]是点M的距离坐标．
根据上述定义，请解答下列问题：
如图②，平面直角坐标系xoy内，直线l1的关系式为y=x，直线l2的关系式为y=
1
2
x，M是平面直角坐标系内的点．
（1）若p=q=0，求距离坐标为[0，0]时，点M的坐标；
（2）若q=0，且p+q=m（m＞0），利用图②，在第一象限内，求距离坐标为[p，q]时，点M的坐标；
（3）若p=1，q=
1
2
，则坐标平面内距离坐标为[p，q]时，点M可以有几个位置？并用三角尺在图③画出符合条件的点M（简要说明画法）．
精英家教网
22、在平面直角坐标系内，点A的横坐标、纵坐标合起来叫点A的
坐标
，它是一对
有序实数对
．
（2012•道里区二模）如图，在平面直角坐标系内，点O为坐标原点，直线y=
1
2
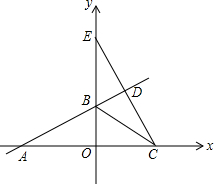x+3交x轴于点A，交y轴于点B点C（4，O），过点C作AB的垂CD，点D为垂足，直线CD交y轴于点E，
（1）求点E的坐标．
（2）连接AE，动点P从点A出发以1个单位/秒的速度沿AC向终点C运动，过点P作PP1∥CE交AE于点P1，设点P（点P不与点A，C重合时）运动的时间为t秒，PP1的长为y，求y与t之间的函数关系式（直接写出自变量t的取值范围）；
（3）在（2）的条件下，点Q为P1E中点，连接DQ，当t为何值时有
PP1
DQ
=
2
5
？并求出此时同时经过P、O、E三点的圆的面积．
在平面直角坐标系内，点O为坐标原点，直线y=
1
2
x+6交x轴于点A，交y轴于点B，过点B作AB的垂线交x轴于点C，∠ABC的平分线交AC于点D．
（1）求点D的坐标；
（2）若P从点A出发以每秒
5
个单位长度的速度向终点B运动，过点P作x轴的平行线交BD于点E，交BC于点F，设线段EF的长为y，点P运动的时间为t（t＞0）秒，求y与t之间的函数关系式，不需写出自变量t的取值范围．
（3）在（2）的条件下，设同时经过B，C，D三点的圆交AB于B，G两点，当t为何值时有EF=
5
3
PG？
在平面直角坐标系内，点P在第一象限，若点P到每条坐标轴的距离都是3，则点P的坐标为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网