题目内容
（2010•松江区二模）在半径为13的圆中，弦AB的长为24，则弦AB的弦心距为 ．
【答案】分析：已知半径和弦长，过圆心作弦的弦心距，利用勾股定理求得弦心距为5．
解答：
解：根据题意画出图形如图示，
过点O作OC⊥AB于C，
则AC=CB，
∵AB=24，
∴AC=CB=12，
在Rt△AOC中，OC=
．
故应填5．
点评：解决与弦有关的问题时，往往需构造以半径、弦心距和弦长的一半为三边的直角三角形，若设圆的半径为r，弦长为a，这条弦的弦心距为d，则有等式r2=d2+（
）2成立，知道这三个量中的任意两个，就可以求出另外一个．
解答：
解：根据题意画出图形如图示，过点O作OC⊥AB于C，
则AC=CB，
∵AB=24，
∴AC=CB=12，
在Rt△AOC中，OC=
．故应填5．
点评：解决与弦有关的问题时，往往需构造以半径、弦心距和弦长的一半为三边的直角三角形，若设圆的半径为r，弦长为a，这条弦的弦心距为d，则有等式r2=d2+（
）2成立，知道这三个量中的任意两个，就可以求出另外一个． 
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
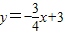分别与x轴、y轴交于点A和点B，二次函数y=ax2-4ax+c的图象经过点B和点C（-1，0），顶点为P．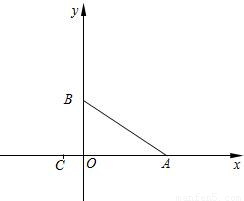
-
= ．