题目内容
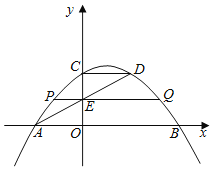
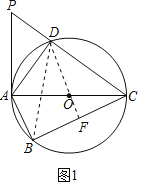
【题目】如图1,四边形![]() 内接于圆
内接于圆![]() ,
,![]() 是圆
是圆![]() 的直径,过点
的直径,过点![]() 的切线与
的切线与![]() 的延长线相交于点
的延长线相交于点![]() .且
.且![]()
(1)求证:![]() ;
;
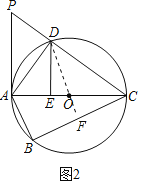
(2)过图1中的点![]() 作
作![]() ,垂足为
,垂足为![]() (如图2),当
(如图2),当![]() ,
,![]() 时,求圆
时,求圆![]() 的半径.
的半径.

【答案】(1)见解析;(2)![]()
【解析】
(1)作DF⊥BC于F,连接DB,根据切线的性质得到∠PAC=90°,根据圆周角定理得到∠ADC=90°,得到∠DBC=∠DCB,得到DB=DC,根据线段垂直平分线的性质、圆周角定理证明即可;
(2)根据垂径定理求出FC,证明△DEC≌△CFD,根据全等三角形的性质得到DE=FC=3,根据射影定理计算即可.
(1)证明:作![]() 于
于![]() ,连接
,连接![]() ,
,
∵![]() 是圆
是圆![]() 的切线,
的切线,
∴![]() ,即
,即![]() ,
,
∵![]() 是圆
是圆![]() 的直径,
的直径,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴![]() 经过点
经过点![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)解:∵![]() 经过点
经过点![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
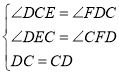 ,
,
∴![]() ≌
≌![]()
![]()
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
则![]() ,
,
∴![]() ,
,
∴圆![]() 的半径为
的半径为![]() .
.

练习册系列答案
相关题目