题目内容
10.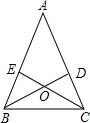 如图,已知AB=AC,BE=CD.
如图,已知AB=AC,BE=CD.(1)说明:BD=CE;
(2)说明:OD=OE.
分析 (1)根据线段的和差得到AD=AE,通过三角形全等即可得到结果.
(2)通过△ABD≌△ACE,可得角相等,根据等腰三角形的性质可得结论.
解答 证明:(1)∵AB=AC,BD=CE,
∴AB-BE=AC-DC,
即AD=AE
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠A=∠A}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE,
∴BD=CE;
(2)由(1)证得△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠ABC=∠ACB,
∴∠DBC=∠ECB,
∴OB=OC,
∴BD-BO=CE-CO,
即OD=OE.
点评 本题考查了等腰三角形的性质和判定,全等三角形的判定与性质,熟练掌握定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.方程x(x+1)=5(x+1)的根是( )
| A. | -1 | B. | 5 | C. | 1 或5 | D. | -1或5 |
18.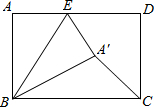 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )
 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )| A. | 3或4$\sqrt{2}$ | B. | 4或3$\sqrt{2}$ | C. | 3或4 | D. | 3$\sqrt{2}$或4$\sqrt{2}$ |
2.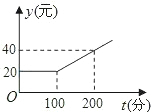 有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:
有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:
(1)通话时间为多少时,两家公司的收费是相同的?
(2)李女士想买一部手机,如果她的月通话时间不超过100分钟,她选择哪家通讯公司更合算?如果她的月通话时间超过100分钟,又将如何选择?
 有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:
有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:| 月租费 | 通话费 |
| 25元 | 0.15元/分钟 |
(2)李女士想买一部手机,如果她的月通话时间不超过100分钟,她选择哪家通讯公司更合算?如果她的月通话时间超过100分钟,又将如何选择?
20.下列计算正确的是( )
| A. | a4+a4=a8 | B. | (a3)4=a7 | ||
| C. | 12a6b4÷3a2b-2=4a4b2 | D. | (-a3b)2=a6b2 |
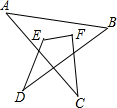 ∠A+∠B+∠C+∠D+∠E+∠F的度数=360°.
∠A+∠B+∠C+∠D+∠E+∠F的度数=360°.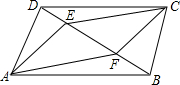 如图,己知AB∥DC,且AB=CD,BF=DE,说明AE∥CF,AF∥CE的理由.
如图,己知AB∥DC,且AB=CD,BF=DE,说明AE∥CF,AF∥CE的理由.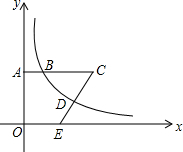 如图所示的平面直角坐标系xOy,点A在y轴正半轴上运动,点B在第一象限,AB⊥y轴,AB=4,在AB的延长点上取一点C,过点C作直线交过点B的双曲线于点D,交x轴正半轴于点E,且CD=DE,设OA=t,四边形OACE的面积为S.
如图所示的平面直角坐标系xOy,点A在y轴正半轴上运动,点B在第一象限,AB⊥y轴,AB=4,在AB的延长点上取一点C,过点C作直线交过点B的双曲线于点D,交x轴正半轴于点E,且CD=DE,设OA=t,四边形OACE的面积为S.