题目内容
17．
如图所示的正方形和长方形卡片若干张，拼成一个长为（a+3b），宽为（2a+b）的矩形，需要这三类卡片共12张．
分析 正方形卡片A类1张，B类6张，以及C类5张．
解答 解：根据题意得：正方形卡片A类1张，B类6张，以及C类5张，
∴需要A类卡片、B类卡片、C类卡片共12张，
故答案为：12
点评 此题考查了整式混合运算的应用，弄清题意是解本题的关键．
练习册系列答案
相关题目
7．已知下列命题：①相等的角是对顶角；②互补的角就是平角；③互补的两个角一定是一个锐角，另一个为钝角；④垂直于同一条直线的两条直线平行；⑤同旁内角的平分线互相垂直．其中真命题的个数为（ ）
| A． | 0 | B． | 1个 | C． | 2个 | D． | 3个 |
5．如果|3x-2|=2-3x，那么x的取值范围是（ ）
| A． | =$\frac{2}{3}$ | B． | ＞$\frac{2}{3}$ | C． | ≤$\frac{2}{3}$ | D． | ≥$\frac{2}{3}$ |
2．
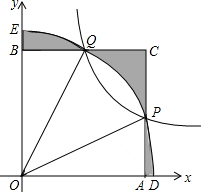如图，反比例函数y=$\frac{k}{x}$（x＞0）图象上一点P（$\sqrt{3}$，1），以点O为圆心，OP长为半径的圆弧交x轴、y轴于D、E两点，交反比例函数的图象于点Q．过点P，Q分别作x轴、y轴的垂线，交于点C，垂足为A，B，则图中阴影部分的面积为（ ）
如图，反比例函数y=$\frac{k}{x}$（x＞0）图象上一点P（$\sqrt{3}$，1），以点O为圆心，OP长为半径的圆弧交x轴、y轴于D、E两点，交反比例函数的图象于点Q．过点P，Q分别作x轴、y轴的垂线，交于点C，垂足为A，B，则图中阴影部分的面积为（ ）| A． | 3+$\frac{π}{6}$-2$\sqrt{3}$ | B． | 3+$\frac{π}{3}$-2$\sqrt{3}$ | C． | 3+$\frac{π}{6}$-$\sqrt{3}$ | D． | 3+$\frac{π}{3}$-$\sqrt{3}$ |
9．如果一个角的补角是120°，那么这个角的余角的度数是（ ）
| A． | 60° | B． | 30° | C． | 90° | D． | 120° |