题目内容
如图,二次函数y=-x2+ax+b的图象与x轴交于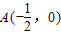 、B(2,0)两点,且与y轴交于点C.
、B(2,0)两点,且与y轴交于点C.(1)求该抛物线的解析式,并判断△ABC的形状;
(2)直接写出不等式-x2+ax+b>0的解集;
(3)在此抛物线上是否存在点P,使得以A、C、B、P四点为顶点的四边形是直角梯形?若存在,请求出点P的坐标;若不存在,说明理由.
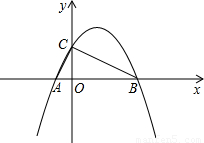
【答案】分析:(1)∵二次函数y=-x2+ax+b的图象经过 、B(2,0)两点,利用待定系数法就可以直接求出a、b的值,求出抛物线的解析式.
、B(2,0)两点,利用待定系数法就可以直接求出a、b的值,求出抛物线的解析式.
(2)不等式-x2+ax+b>0的解集,实际上就是y=-x2+ax+b>0时x的取值范围,利用抛物线与x轴的交点和图象特征就可以求出.
(3)在(1)题已将证得∠ACB=90°,若A、C、B、P四点为顶点的四边形是直角梯形,则有两种情况需要考虑:
①以BC、AP为底,AC为高;可先求出直线BC的解析式,进而可确定直线AP的解析式,联立抛物线的解析式即可求出点P的坐标.
②以AC、BP为底,BC为高;方法同①.
解答:解:(1))∵二次函数y=-x2+ax+b的图象经过 、B(2,0)两点,由题意,得
、B(2,0)两点,由题意,得
 ,解得:
,解得: ,
,
∴抛物线的解析式为:y=-x2+ x+1.
x+1.
∴C(0,1),
∴AC2=AO2+CO2= ,
,
CB2=BO2+CO2=5,
AB2= ,
,
∴AC2+CB2=AB2,
∴△ACB是直角三角形;
(2)由图象得原不等式的解集为:
- <x<2
<x<2
(3)存在,点P( ,-
,- )或(-
)或(- ,-9);
,-9);
若以A、C、B、P四点为顶点的直角梯形以BC、AP为底;
∵B(2,0),C(0,1),
∴直线BC的解析式为:y=- x+1;
x+1;
 设过点B且平行于AC的直线的解析式为y=-
设过点B且平行于AC的直线的解析式为y=- x+h,
x+h,
将点A(- ,0)代入得:(-
,0)代入得:(- )×(-
)×(- )+h=0,h=-
)+h=0,h=- ;
;
∴y=- x-
x- ;
;
联立抛物线的解析式有:
 ,
,
解得 ,
, ;
;
∴点P( ,-
,- );
);
若以A、C、B、P四点为顶点的直角梯形以AC、BP为底,
同理可求得P(- ,-9);
,-9);
故当P( ,-
,- )或(-
)或(- ,-9)时,以A、C、B、P四点为顶点的四边形是直角梯形.
,-9)时,以A、C、B、P四点为顶点的四边形是直角梯形.
(根据抛物线的对称性求出另一个P点坐标亦可)
点评:本题是一道二次函数的综合试题,考查了待定系数法求抛物线的解析式,相似三角形的判定与性质,二次函数与不等式的关系,直角梯形的运用.
 、B(2,0)两点,利用待定系数法就可以直接求出a、b的值,求出抛物线的解析式.
、B(2,0)两点,利用待定系数法就可以直接求出a、b的值,求出抛物线的解析式.(2)不等式-x2+ax+b>0的解集,实际上就是y=-x2+ax+b>0时x的取值范围,利用抛物线与x轴的交点和图象特征就可以求出.
(3)在(1)题已将证得∠ACB=90°,若A、C、B、P四点为顶点的四边形是直角梯形,则有两种情况需要考虑:
①以BC、AP为底,AC为高;可先求出直线BC的解析式,进而可确定直线AP的解析式,联立抛物线的解析式即可求出点P的坐标.
②以AC、BP为底,BC为高;方法同①.
解答:解:(1))∵二次函数y=-x2+ax+b的图象经过
 、B(2,0)两点,由题意,得
、B(2,0)两点,由题意,得 ,解得:
,解得: ,
,∴抛物线的解析式为:y=-x2+
 x+1.
x+1.∴C(0,1),
∴AC2=AO2+CO2=
 ,
,CB2=BO2+CO2=5,
AB2=
 ,
,∴AC2+CB2=AB2,
∴△ACB是直角三角形;
(2)由图象得原不等式的解集为:
-
 <x<2
<x<2(3)存在,点P(
 ,-
,- )或(-
)或(- ,-9);
,-9);若以A、C、B、P四点为顶点的直角梯形以BC、AP为底;
∵B(2,0),C(0,1),
∴直线BC的解析式为:y=-
 x+1;
x+1; 设过点B且平行于AC的直线的解析式为y=-
设过点B且平行于AC的直线的解析式为y=- x+h,
x+h,将点A(-
 ,0)代入得:(-
,0)代入得:(- )×(-
)×(- )+h=0,h=-
)+h=0,h=- ;
;∴y=-
 x-
x- ;
;联立抛物线的解析式有:
 ,
,解得
 ,
, ;
;∴点P(
 ,-
,- );
);若以A、C、B、P四点为顶点的直角梯形以AC、BP为底,
同理可求得P(-
 ,-9);
,-9);故当P(
 ,-
,- )或(-
)或(- ,-9)时,以A、C、B、P四点为顶点的四边形是直角梯形.
,-9)时,以A、C、B、P四点为顶点的四边形是直角梯形.(根据抛物线的对称性求出另一个P点坐标亦可)
点评:本题是一道二次函数的综合试题,考查了待定系数法求抛物线的解析式,相似三角形的判定与性质,二次函数与不等式的关系,直角梯形的运用.

练习册系列答案
相关题目
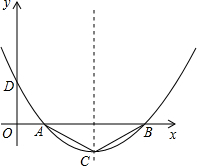 如图,二次函数的图象经过点D(0,
如图,二次函数的图象经过点D(0,
 如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题: 如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b
如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b