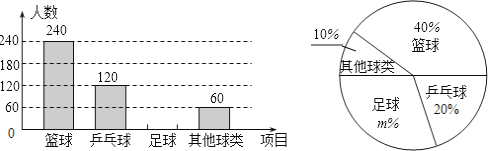
题目内容
【题目】如图，在四边形ABCD中，∠ABC=90°，AB=BC=2 
，E、F分别是AD、CD的中点，连接BE、BF、EF．若四边形ABCD的面积为6，则△BEF的面积为（ ） 
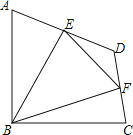
A.2
B.
C.
D.3
【答案】C
【解析】解：连接AC，过B作EF的垂线交AC于点G，交EF于点H，∵∠ABC=90°，AB=BC=2 
，∴AC= 
= 
=4，
∵△ABC为等腰三角形，BH⊥AC，
∴△ABG，△BCG为等腰直角三角形，
∴AG=BG=2
∵S△ABC= 
ABAC= ×2 ×2 =4，
∴S△ADC=2，
∵ 
=2，∴GH= 
BG= 
，∴BH= 
，又∵EF= AC=2，∴S△BEF= EFBH= ×2× = ，
故选C．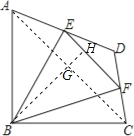
【考点精析】解答此题的关键在于理解三角形的面积的相关知识，掌握三角形的面积=1/2×底×高．
练习册系列答案
相关题目
