题目内容
8.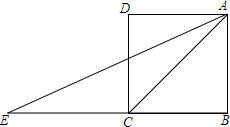 如图,在正方形ABCD中,E是BC延长线上一点,且AC=EC,求∠DAE的度数.
如图,在正方形ABCD中,E是BC延长线上一点,且AC=EC,求∠DAE的度数.
分析 根据正方形的对角线平分一组对角可得∠DAC=∠ACB=45°,再根据等边对等角可得∠E=∠EAC,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠EAC,再根据∠DAE=∠DAC-∠EAC代入数据进行计算即可得解.
解答 解:∵四边形ABCD为正方形,
∴∠DAC=∠ACB=45°,
∵AC=CE,
∴∠E=∠EAC,
∵2∠EAC=∠E+∠EAC=∠ACB=45°,
∴∠EAC=22.5°,
∴∠DAE=∠DAC-∠EAC=45°-22.5°=22.5°.
点评 本题考查了正方形的性质,主要利用了正方形的对角线平分一组对角,等边对等角的性质,三角形的外角性质,是基础题,熟记各性质是解题的关键.

练习册系列答案
相关题目
10.“十•一”黄金周期间,九寨沟风景区在7天假期中每天旅游的人数变化如表:(正数表示比9月30日多的人数,负数表示比9月30日少的人数):
(1)若9月30日的游客人数记为a万人,请用含a的代数式表示10月2日的游客人数;
(2)请判断7天内游客人数最多和最少的各是哪一天,它们相差多少万人?
(2)若a=2,平均每人消费300元,请问风景区在这7天内总收入多少万元?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 (万人) | +1.7 | +0.9 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)请判断7天内游客人数最多和最少的各是哪一天,它们相差多少万人?
(2)若a=2,平均每人消费300元,请问风景区在这7天内总收入多少万元?
3.(1)先求出下列各组数据的平均数和方差;
①1,2,3,4,5,6,7,8,9;
②11,12,13,14,15,16,17,18,19,;
③10,20,30,40,50,60,70,80,90.
(2)根据上面的计算结果,你能发现什么规律,按你的发现填写下表:
①1,2,3,4,5,6,7,8,9;
②11,12,13,14,15,16,17,18,19,;
③10,20,30,40,50,60,70,80,90.
(2)根据上面的计算结果,你能发现什么规律,按你的发现填写下表:
| 数 据 | 平均数 | 方差 |
| x1,x2,…,xn | $\overline{X}$ | S2 |
| x1+a,x2+a,…,xn+a | $\overline{x}$+a | S2 |
| mx1,mx2,…,mxn | m$\overline{x}$ | m2S2 |
13.在数字1001000100010000中,0出现的频率是( )
| A. | 0.75 | B. | 0.8 | C. | 0.5 | D. | 12 |
20.下列说法中,正确的是( )
| A. | 0是最小的整数 | B. | 最大的负整数是-1 | ||
| C. | 任何有理数的绝对值都是正数 | D. | 一个有理数的平方总是正数 |
17. 如图,在平面直角坐标系中.矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.如果OA=3,OC=2,则经过点E的反比例函数解析式为( )
如图,在平面直角坐标系中.矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.如果OA=3,OC=2,则经过点E的反比例函数解析式为( )
 如图,在平面直角坐标系中.矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.如果OA=3,OC=2,则经过点E的反比例函数解析式为( )
如图,在平面直角坐标系中.矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.如果OA=3,OC=2,则经过点E的反比例函数解析式为( )| A. | $y=\frac{9}{2x}$ | B. | $y=\frac{2}{9x}$ | C. | $y=\frac{{\sqrt{13}}}{x}$ | D. | $y=\frac{{\sqrt{13}}}{2x}$ |
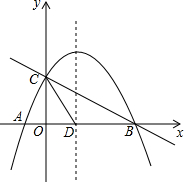 如图,直线y1=-$\frac{1}{2}$x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(-1,0).
如图,直线y1=-$\frac{1}{2}$x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(-1,0).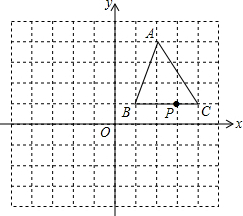 如图,三角形ABC的顶点坐标分别为A(2,4)、B(1,1)、C(4,1).BC上的一点P的坐标为P(3,1),将三角形ABC向左平移4个单位,再向上平移1个单位,得到三角形A1B1C1,其中点A、B、C、P分别对应点A1、B1、C1、P1.
如图,三角形ABC的顶点坐标分别为A(2,4)、B(1,1)、C(4,1).BC上的一点P的坐标为P(3,1),将三角形ABC向左平移4个单位,再向上平移1个单位,得到三角形A1B1C1,其中点A、B、C、P分别对应点A1、B1、C1、P1.