题目内容
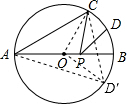
如图，AB是⊙O的直径，AB=2，点C在⊙O上，∠CAB=30°，D为
的中点，点P是直径AB上一动点，则PC+PD的最小值是（ ）
 |
| BC |
| A．1 | B．
| C．
| D．
|
作出D关于AB的对称点D′，连接OC，OD′，CD′．
又∵点C在⊙O上，∠CAB=30°，D为
的中点，即
=
，
∴∠BAD′=
∠CAB=15°．
∴∠CAD′=45°．
∴∠COD′=90°．则△COD′是等腰直角三角形．
∵OC=OD′=
AB=1，
∴CD′=
．
故选B．
又∵点C在⊙O上，∠CAB=30°，D为
|
| BC |
|
| BD |
|
| BD′ |
∴∠BAD′=
| 1 |
| 2 |
∴∠CAD′=45°．
∴∠COD′=90°．则△COD′是等腰直角三角形．
∵OC=OD′=
| 1 |
| 2 |
∴CD′=
| 2 |
故选B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
