题目内容
点P(2,a)在函数 的图象上,斜边OA(O为坐标中心)在x轴上,且△OPA是等腰直角三角形,则a=________,点A的坐标为________.
的图象上,斜边OA(O为坐标中心)在x轴上,且△OPA是等腰直角三角形,则a=________,点A的坐标为________.
-2 (4,0)
分析:把点P的坐标代入函数解析式可以求得a=-2.过P作PB⊥x轴于B,根据等腰直角三角形的性质得到BP=BO=BA,设OB=a,则P点坐标为(a,a),把它代入y= (x>0)可求得a的值,而OA=2a,从而确定A点坐标.
(x>0)可求得a的值,而OA=2a,从而确定A点坐标.
解答: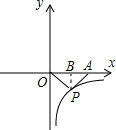 解:过P作PB⊥x轴于B,如图
解:过P作PB⊥x轴于B,如图
∵△POA是等腰直角三角形,
∴BP=BO=BA,
设OB=a,则P点坐标为(a,a),
∵点P在函数y= 的图象上,
的图象上,
∴a2=4,
∴a=2,
∴OA=2a=4,
∴A点坐标为(4,0).
故答案为-2;(4,0).
点评:本题考查了点在反比例函数图象上,则点的横纵坐标满足反比例的解析式.也考查了等腰直角三角形的性质.
分析:把点P的坐标代入函数解析式可以求得a=-2.过P作PB⊥x轴于B,根据等腰直角三角形的性质得到BP=BO=BA,设OB=a,则P点坐标为(a,a),把它代入y=
 (x>0)可求得a的值,而OA=2a,从而确定A点坐标.
(x>0)可求得a的值,而OA=2a,从而确定A点坐标.解答:
 解:过P作PB⊥x轴于B,如图
解:过P作PB⊥x轴于B,如图∵△POA是等腰直角三角形,
∴BP=BO=BA,
设OB=a,则P点坐标为(a,a),
∵点P在函数y=
 的图象上,
的图象上,∴a2=4,
∴a=2,
∴OA=2a=4,
∴A点坐标为(4,0).
故答案为-2;(4,0).
点评:本题考查了点在反比例函数图象上,则点的横纵坐标满足反比例的解析式.也考查了等腰直角三角形的性质.

练习册系列答案
相关题目
若点A(2,4)在函数y=kx-2的图象上,则下列各点在函数图象上的是( )
| A、(0,-2) | ||||
B、(
| ||||
| C、(8,20) | ||||
D、(
|
 如图,点p1、P2、P3…Pn在函数
如图,点p1、P2、P3…Pn在函数