题目内容
下列结论正确的是( )
分析:根据正比例函数的定义对A进行判断;根据一次函数的定义对B进行判断;根据一次函数图象上点的坐标特征对C、D进行判断.
解答:解:A、正比例函数是特殊的一次函数,所以A选项正确;
B、函数y=
-b(k≠0,b是常数)是一次函数,所以B选项错误;
C、直线y=-x-b与y轴的交点坐标为(0,-b),而b的值不确定,所以C选项错误;
D、点P(-2,-2)不在函数y=-2x-2的图象上.
故选A.
B、函数y=
| x |
| k |
C、直线y=-x-b与y轴的交点坐标为(0,-b),而b的值不确定,所以C选项错误;
D、点P(-2,-2)不在函数y=-2x-2的图象上.
故选A.
点评:本题考查了一次函数图象上点的坐标特征:一次函数图象上点的坐标满足其解析式.也考查了一次函数的定义和正比例函数定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列结论正确的是( )
A、
| ||
B、当x=-3时,分式
| ||
| C、(-a+b)(-a-b)=a2-b2 | ||
| D、a2+a3=a5 |
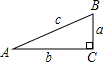 如图,在Rt△ABC中,∠C=90°,BC=a,CA=b,AB=C,则下列结论正确的是( )
如图,在Rt△ABC中,∠C=90°,BC=a,CA=b,AB=C,则下列结论正确的是( )A、sinB=
| ||
B、cosB=
| ||
C、tanB=
| ||
D、cotB=
|
如果-b是a的立方根(ab≠0),那么下列结论正确的是( )
| A、-b也是-a的立方根 | B、b是a的立方根 | C、b是-a的立方根 | D、以上结论均不正确 |
