题目内容
 17、如图,在平面内将△ABC绕点A逆时针旋转至△AB'C',使CC'∥AB,如果∠BAC=70°,那么旋转角α的度数为( )
17、如图,在平面内将△ABC绕点A逆时针旋转至△AB'C',使CC'∥AB,如果∠BAC=70°,那么旋转角α的度数为( )分析:根据旋转的性质可得出AC=AC',然后根据CC'∥AB,∠BAC=70°,可得出∠AC'C的度数,进而根据等腰三角形的性质可得出答案.
解答:解:由题意得:AC=AC',
∴△ACC'是等腰三角形,
又CC'∥AB,
∴AC'C=∠BAC=70°,
∴∠CAC'=40°,即旋转角度α的度数为40°.
故选B.
∴△ACC'是等腰三角形,
又CC'∥AB,
∴AC'C=∠BAC=70°,
∴∠CAC'=40°,即旋转角度α的度数为40°.
故选B.
点评:本题考查旋转的性质与等腰三角形的性质,属于基础题,难度一般,解答本题的关键是掌握旋转前后对应线段相等、对应角相等.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
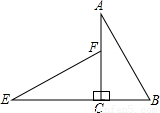
 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB= 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=
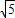 ,BC=1,则线段BE的长为 .
,BC=1,则线段BE的长为 .