题目内容
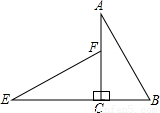
 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=2
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=2| 5 |
| 2 |
3
| 2 |
3
,AF=| 2 |
2
| 2 |
2
.| 2 |
分析:首先利用勾股定理可以计算出AC的长,再根据旋转可得EC=AC,BC=FC,再利用线段的和差关系可得答案.
解答:解:∵在Rt△ABC中,AB=2
,BC=
,
∴AC=
=
=3
,
根据旋转可得FC=BC=
,EC=AC=3
,
∴AF=AC-FC=3
-
=2
,
故答案为:3
,2
.
| 5 |
| 2 |
∴AC=
| AB2-BC2 |
| 18 |
| 2 |
根据旋转可得FC=BC=
| 2 |
| 2 |
∴AF=AC-FC=3
| 2 |
| 2 |
| 2 |
故答案为:3
| 2 |
| 2 |
点评:此题主要考查了旋转的性质,以及勾股定理的应用,关键是掌握旋转后哪些线段是对应相等的.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=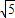 ,BC=1,则线段BE的长为 .
,BC=1,则线段BE的长为 .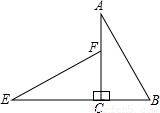
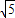 ,BC=1,则线段BE的长为 .
,BC=1,则线段BE的长为 .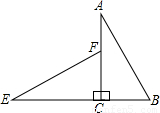
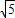 ,BC=1,则线段BE的长为 .
,BC=1,则线段BE的长为 .