Question

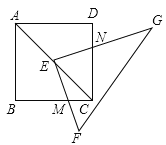
【题目】如图，若△ABC内一点P满足∠PAC＝∠PCB＝∠PBA，则称点P为△ABC的布罗卡尔点，已知△ABC中，CA＝CB，∠ACB＝120°，P为△ABC的布罗卡尔点，若，则PB+PC＝_____．

Answer 1

【答案】1+

【解析】

作CH⊥AB于H,首先证明AB＝BC,再证明△PAB∽△PBC,可得

,即可求出PB、PC.

解：作CH⊥AB于H．

∵CA＝CB,CH⊥AB,∠ACB＝120°,

∴AH＝BH,∠ACH＝∠BCH＝60°,∠CAB＝∠CBA＝30°,

∴AB＝2BH＝2BCcos30°＝BC,

∵∠PAC＝∠PCB＝∠PBA,

∴∠PAB＝∠PBC,

∴△PAB∽△PBC,

∴,

∴PA＝,

∴PB＝1,PC＝,

∴PB+PC＝1+,

故答案为:1+.