题目内容
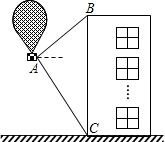 (2012•工业园区一模)如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.
(2012•工业园区一模)如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.(1)请你计算该楼的高度;
(2)为了安全飞越高楼,气球先上升,然后再沿水平方向接近楼顶B处,求气球行驶到B处的路程.
(结果保留根号,参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
分析:(1)过A作AD⊥CB,垂足为点D,在Rt△ADC中利用锐角三角函数的定义可求出AD的长,同理在Rt△ADB中利用BD=AD×tan37°即可求出该楼的高度;
(2)再利用AD,BD的值求出气球行驶到B处的路程即可.
(2)再利用AD,BD的值求出气球行驶到B处的路程即可.
解答: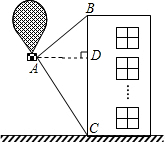 解:(1)过点A作AD⊥CB,垂足为点D,
解:(1)过点A作AD⊥CB,垂足为点D,
在Rt△ADC中,
∵CD=36m,∠CAD=60°,
∴AD=
=
=12
(m),
在Rt△ADB中,∵AD=12
,∠BAD=37°,
∴BD=AD×tan37°=12
×0.75=9
(m),
故该楼的高度=CD+BD=(36+9
)m;
答:该楼的高度为36+9
m;
(2)气球行驶到B处的最短路程=AD+BD=12
+9
=21
(m),
答:气球行驶到B处的最短路程为21
米.
 解:(1)过点A作AD⊥CB,垂足为点D,
解:(1)过点A作AD⊥CB,垂足为点D,在Rt△ADC中,
∵CD=36m,∠CAD=60°,
∴AD=
| CD |
| tan60° |
| 36 | ||
|
| 3 |
在Rt△ADB中,∵AD=12
| 3 |
∴BD=AD×tan37°=12
| 3 |
| 3 |
故该楼的高度=CD+BD=(36+9
| 3 |
答:该楼的高度为36+9
| 3 |
(2)气球行驶到B处的最短路程=AD+BD=12
| 3 |
| 3 |
| 3 |
答:气球行驶到B处的最短路程为21
| 3 |
点评:本题考查的是解直角三角形的应用,解答此题的关键是作出辅助线,利用锐角三角函数的定义求出AD及BD的长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•工业园区一模)如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D为x轴上动点,若CD=3AB,四边形ABCD的面积为4,则这个反比例函数的解析式为
(2012•工业园区一模)如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D为x轴上动点,若CD=3AB,四边形ABCD的面积为4,则这个反比例函数的解析式为 (2012•工业园区一模)如图:二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于C点,若AC⊥BC,则a的值为( )
(2012•工业园区一模)如图:二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于C点,若AC⊥BC,则a的值为( ) (2012•工业园区一模)如图,等腰△AEF的腰长与菱形ABCD的边长相等,其底边上的点E、F分别在BC、CD上,若∠EAF=63°,则∠B=
(2012•工业园区一模)如图,等腰△AEF的腰长与菱形ABCD的边长相等,其底边上的点E、F分别在BC、CD上,若∠EAF=63°,则∠B=