题目内容
已知关于x的方程x2﹣(2k﹣3)x+k2+1=0有两个不相等的实数根x1、x2.
(1)求k的取值范围;
(2)试说明x1<0,x2<0;
(3)若抛物线y=x2﹣(2k﹣3)x+k2+1与x轴交于A、B两点,点A、点B到原点的距离分别为OA、OB,且OA+OB=2OA•OB﹣3,求k的值.
解:(1)由题意可知:△=【﹣(2k﹣3)】2﹣4(k2+1)>0,
即﹣12k+5>0
∴ .
.
(2)∵ ,
,
∴x1<0,x2<0.
(3)依题意,不妨设A(x1,0),B(x2,0).
∴OA+OB=|x1|+|x2|=﹣(x1+x2)=﹣(2k﹣3),
OA•OB=|﹣x1||x2|=x1x2=k2+1,
∵OA+OB=2OA•OB﹣3,
∴﹣(2k﹣3)=2(k2+1)﹣3,
解得k1=1,k2=﹣2.
∵ ,
,
∴k=﹣2.

练习册系列答案
相关题目
如图,在半径为6cm的⊙O中,点A是劣弧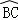 的中点,点D是优弧
的中点,点D是优弧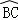 上一点,且∠D=30°,下列四个结论:
上一点,且∠D=30°,下列四个结论:
①OA⊥BC;②BC=6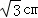 ;③sin∠AOB=
;③sin∠AOB=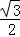 ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.
其中正确结论的序号是( )

|
| A. | ①③ | B. | ①②③④ | C. | ②③④ | D. | ①③④ |
某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
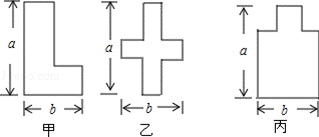
|
| A. | 甲种方案所用铁丝最长 | B. | 乙种方案所用铁丝最长 |
|
| C. | 丙种方案所用铁丝最长 | D. | 三种方案所用铁丝一样长 |





 )﹣1﹣|﹣5|+(
)﹣1﹣|﹣5|+( ﹣2)0
﹣2)0 经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为 .
经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为 .

 ﹣2,则(x+y)y=
﹣2,则(x+y)y=