题目内容
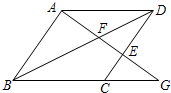如图，已知菱形ABCD，点G在BC的延长线上，连接AG，与边CD交于点E，与对角线BD交于点F，求证：AF2=EF•FG．
证明：【法一】：∵菱形ABCD
∴AD∥BG，AB∥CD
∴
，
=
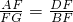可得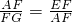
，即AF2=FE•FG
【法二】：连接CF，
∵菱形ABCD，证得CF=AF，
证明△FCE∽△FGC，
可得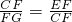
，从而CF2=FE•FG
即AF2=FE•FG
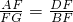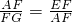分析：由菱形ABCD得两组比例线段，=，则，即AF2=FE•FG．
点评：本题考查了菱形的性质、相似三角形的判定和性质，是基础知识要熟练掌握．
∴AD∥BG，AB∥CD
∴
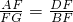，=可得
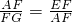，即AF2=FE•FG【法二】：连接CF，
∵菱形ABCD，证得CF=AF，
证明△FCE∽△FGC，
可得
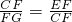，从而CF2=FE•FG即AF2=FE•FG
分析：由菱形ABCD得两组比例线段
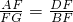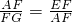，=，则，即AF2=FE•FG．点评：本题考查了菱形的性质、相似三角形的判定和性质，是基础知识要熟练掌握．
练习册系列答案
相关题目
如图，已知菱形ABCD的边长为1.5cm，B，C两点在扇形AEF的
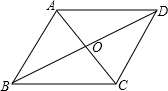如图，已知菱形ABCD的周长为16cm，∠ABC=60°，对角线AC和BD相交于点O，求AC和BD的长．
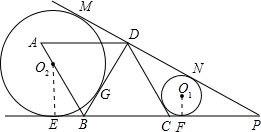上，半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N，半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G．
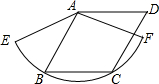如图，已知菱形ABCD为2cm．B、C两点在以点A为圆心的