题目内容
如图，D是△ABC边上一点，在条件：①∠ACB=∠B；②AC2=AD•AB；③BC•AC=CD•AB；④∠B=∠ACD中选取一个就能使△ABC∽△ACD，这样的条件个数有
- A.1
- B.2
- C.3
- D.4
B
分析：两组角对应相等的两个三角形互为相似三角形，两边对应成比例且夹角相等的三角形互为相似三角形．
解答：∵AC2=AD•AB，∠A=∠A，
∴△ABC∽△ACD．
∵∠B=∠ACD，∠A=∠A，
∴△ABC∽△ACD．
故有两个这样的条件．
故选B．
点评：本题考查相似三角形的判定定理，本题主要考查了两组角对应相等的两个三角形互为相似三角形，两边对应成比例且夹角相等的三角形互为相似三角形．
分析：两组角对应相等的两个三角形互为相似三角形，两边对应成比例且夹角相等的三角形互为相似三角形．
解答：∵AC2=AD•AB，∠A=∠A，
∴△ABC∽△ACD．
∵∠B=∠ACD，∠A=∠A，
∴△ABC∽△ACD．
故有两个这样的条件．
故选B．
点评：本题考查相似三角形的判定定理，本题主要考查了两组角对应相等的两个三角形互为相似三角形，两边对应成比例且夹角相等的三角形互为相似三角形．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
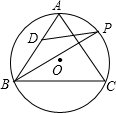如图，D是△ABC边AB上的一点，使得AB=3AD，P是△ABC外接圆上一点（P在弧AC上），使得∠ADP=∠ACB，求
4、如图，D是△ABC边AC上的一点，过D点画线段DE，使点E在△ABC的边上，并且点D，E和△ABC的一个顶点组所在小三角形与△ABC相似，则这样的E点有
如图，P是△ABC边AB上的一点，连接CP，下列条件中，不能判定△ACP∽△ABC的是（ ）| A、AC2=AP•AB | ||||
| B、∠ABC=∠ACP | ||||
| C、∠APC=∠ACB | ||||
D、
|
如图，E是△ABC边BC上的一点，DE垂直平分AB，△ACE的周长是8.5，AB=3，则△ABC的周长为（ ）
已知：如图，D是△ABC边BC上的一点，∠DAC=∠B，