题目内容
我们把分子为1的分数叫理想分数,如: ,
, ,
, ,…,任何一个理想分数都可以写成两个不同理想分数的和,如:
,…,任何一个理想分数都可以写成两个不同理想分数的和,如: ;
; ;
; ;…,根据对上述式子的观察,请你思考:
;…,根据对上述式子的观察,请你思考:
(1)如果理想分数 ,
, ,那么a=______,b=______;
,那么a=______,b=______;
如果理想分数 ,
, ,那么x=______,y=______;
,那么x=______,y=______;
(2)运用你观察到的规律计算:(要写过程)
① ; ②
; ② ;
;
(3)
①如果理想分数 (n是不小于2的正整数),那么c+d=______(用含n的式子表示);
(n是不小于2的正整数),那么c+d=______(用含n的式子表示);
②如果理想分数 (m是不小于3的正整数,m<f),那么e+f=______(用含m的式子表示).
(m是不小于3的正整数,m<f),那么e+f=______(用含m的式子表示).
解:(1)∵分数 ,
, ,
,
∴a=30,b=10;
∵ ,
, ,
,
∴x=6,y=132;
故答案为:30,10;6,132;
(2)运用你观察到的规律计算:(要写过程)
①
=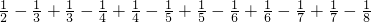
=
= ,
,
②
=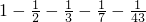
=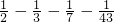
=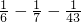
=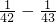
=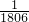 ,
,
(3)①∵ =
= +
+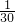 ,
, =
= +
+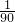 ,
, ,
,
∴c+d=(n+1)2;
故答案为:(n+1)2;
②∵ ,
, ,x=6,y=132,
,x=6,y=132, ,
,
∴e+f=m2-1.
故答案为:m2-1.
分析:(1)利用分数的加减运算法则得出即可;
(2)①利用 =
= -
- ,
, =
= -
- …进而求出即可;
…进而求出即可;
②直接去括号,利用有理数的加减运算法则得出即可.
(3)①利用(1)中所求得出规律进而求出即可;
②利用(1)中所求得出规律进而求出即可.
点评:此题主要考查了数字变化规律以及新概念问题,根据已知得出数字变化规律是解题关键.
 ,
, ,
,∴a=30,b=10;
∵
 ,
, ,
,∴x=6,y=132;
故答案为:30,10;6,132;
(2)运用你观察到的规律计算:(要写过程)
①

=
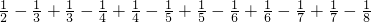
=

=
 ,
,②

=
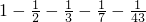
=
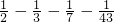
=
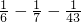
=
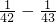
=
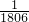 ,
,(3)①∵
 =
= +
+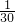 ,
, =
= +
+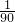 ,
, ,
,∴c+d=(n+1)2;
故答案为:(n+1)2;
②∵
 ,
, ,x=6,y=132,
,x=6,y=132, ,
,∴e+f=m2-1.
故答案为:m2-1.
分析:(1)利用分数的加减运算法则得出即可;
(2)①利用
 =
= -
- ,
, =
= -
- …进而求出即可;
…进而求出即可;②直接去括号,利用有理数的加减运算法则得出即可.
(3)①利用(1)中所求得出规律进而求出即可;
②利用(1)中所求得出规律进而求出即可.
点评:此题主要考查了数字变化规律以及新概念问题,根据已知得出数字变化规律是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目