Question

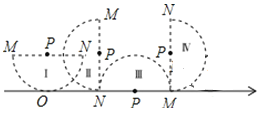
【题目】如图，有一直径MN=4的半圆形纸片，其圆心为点P，从初始位置Ⅰ开始，在无滑动的情况下沿数轴向右翻滚至位置Ⅳ，其中位置Ⅰ中的MN平行于数轴，且半⊙P与数轴相切于原点O；位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上.

解答下列问题：

(1)位置Ⅰ中的MN与数轴之间的距离为____________；

（2）位置Ⅱ中的半⊙P与数轴的位置关系是________；

（3）求位置Ⅲ中的圆心P在数轴上表示的数；

（4）纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时，求该纸片所扫过图形的面积.

Answer 1

【答案】（1）2；（2）相切；（3）；（4）扫过的图形面积=

【解析】

（1）由圆的性质即可求解；

（2）由（1）中圆的半径，再根据切线的性质进行解答；

（3）根据位置Ⅰ中的长与数轴上线段ON相等求出的长，再根据弧长公式求出的长，进而可得出结论；

（4）作NC垂直数轴于点C，作PH⊥NC于点H，连接PA，则四边形PHCA为矩形，在Rt△NPH中，根据sin∠NPH==即可∠NPH、∠MPA的度数，进而可得出的长.

（1）∵⊙P的直径=4，

∴⊙P的半径=2；

（2）∵⊙P与直线有一个交点，

∴位置Ⅰ中的MN与数轴之间的距离为2，位置Ⅱ中的半⊙P与数轴的位置关系是相切；

（3）位置Ⅰ中的长与数轴上线段ON相等，

∵的长为=π，NP=2，

∴位置Ⅲ中的圆心P在数轴上表示的数为π+2；

（3）点N所经过路径长为=2π，

S半圆==2π，S扇形==4π，

故半⊙P所扫过图形的面积为2π+4π=6π．