题目内容

梯形ABCD的两条对角线AC与BD交于E，若S_△DCE与S_△DCB之比为1：3，则S_△ABE与S_△ABD的比为________．

2：3
分析：已知△DCE和△DCB的面积比，由于这两个三角形等高，因此它们的面积比等于底边的比；因此BE：BD=2：3，又因为△ABE和△ABD中，BE和BD边上的高相同，所以面积比等于对应的底之比，由此可求出△ABE和△ABD的面积比．
解答：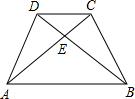

解：∵S_△DCE：S_△DCB=1：3，
∴DE：BD=1：3，
即BE：BD=2：3，
∵△ABE和△ABD中，BE和BD边上的高相同，
∴S_△ABE：S_△ABD=BE：BD=2：3．
故答案为：2：3
点评：本题考查了梯形的性质、两平行线间三角形的性质，以及高相等的三角形面积比可以转化为其对应高边上的底之比和同底等高的两个三角形的面积相等．