题目内容
如果点P在坐标轴上,以P为圆心, 为半径的圆与直线y=-
为半径的圆与直线y=- x+2
x+2 相切于C点,则过点C的双曲线的K是 .
相切于C点,则过点C的双曲线的K是 .
【答案】分析:过点O作直线AB的垂线,垂足为C点.由直线解析式可知,OA=2,OB=2 ;然后利用三角形的面积公式求得OC=
;然后利用三角形的面积公式求得OC= ;再根据∠CAO的三角函数值即可求得点C的坐标,则过点C的双曲线的K=xy.进而算出k的值.
;再根据∠CAO的三角函数值即可求得点C的坐标,则过点C的双曲线的K=xy.进而算出k的值.
解答: 解:过点O作直线AB的垂线,垂足为C点,
解:过点O作直线AB的垂线,垂足为C点,
∵直线y=- x+2
x+2 与x轴交于A,与y轴交于B,
与x轴交于A,与y轴交于B,
∴A(2,0),B(0,2 ),
),
∴OA=2,OB=2 ,
,
由勾股定理可知:AB=4,
S△AOB= OC•AB=
OC•AB= OA•OB,
OA•OB,
 CO×4=
CO×4= 2×2
2×2 ,
,
∴OC= ,
,
∵以P为圆心, 为半径的圆,
为半径的圆,
∴P(0,0),根据中心对称性得点P′(4,0),
①当P(0,0)时,过C作CD⊥x轴,CE⊥y轴,
∵CO= ,AO=2,
,AO=2,
∴sin∠CAO=
∴∠CAO=60°,
∴∠COD=30°,
∴CD= ,
,
∴DO= ,
,
∴C( ,
, ),
),
设过C点的双曲线关系式为y= (k≠0),
(k≠0),
∴K= ×
× =
= ;
;
②当P′(4,0)时,过C作CG⊥x轴,CH⊥y轴,
与①同理可得:P′G= ,GC′=
,GC′= ,
,
∴C′( ,-
,- ),
),
设过C′点的双曲线关系式为y= (k≠0),
(k≠0),
K= ×(-
×(- )=-
)=- ,
,
故答案为: 或-
或- .
.
点评:此题主要考查了直线与圆的位置关系,解决问题的关键是根据题意确定出P点的坐标.
 ;然后利用三角形的面积公式求得OC=
;然后利用三角形的面积公式求得OC= ;再根据∠CAO的三角函数值即可求得点C的坐标,则过点C的双曲线的K=xy.进而算出k的值.
;再根据∠CAO的三角函数值即可求得点C的坐标,则过点C的双曲线的K=xy.进而算出k的值.解答:
 解:过点O作直线AB的垂线,垂足为C点,
解:过点O作直线AB的垂线,垂足为C点,∵直线y=-
 x+2
x+2 与x轴交于A,与y轴交于B,
与x轴交于A,与y轴交于B,∴A(2,0),B(0,2
 ),
),∴OA=2,OB=2
 ,
,由勾股定理可知:AB=4,
S△AOB=
 OC•AB=
OC•AB= OA•OB,
OA•OB, CO×4=
CO×4= 2×2
2×2 ,
,∴OC=
 ,
,∵以P为圆心,
 为半径的圆,
为半径的圆,∴P(0,0),根据中心对称性得点P′(4,0),
①当P(0,0)时,过C作CD⊥x轴,CE⊥y轴,
∵CO=
 ,AO=2,
,AO=2,∴sin∠CAO=

∴∠CAO=60°,
∴∠COD=30°,
∴CD=
 ,
,∴DO=
 ,
,∴C(
 ,
, ),
),设过C点的双曲线关系式为y=
 (k≠0),
(k≠0),∴K=
 ×
× =
= ;
;②当P′(4,0)时,过C作CG⊥x轴,CH⊥y轴,
与①同理可得:P′G=
 ,GC′=
,GC′= ,
,∴C′(
 ,-
,- ),
),设过C′点的双曲线关系式为y=
 (k≠0),
(k≠0),K=
 ×(-
×(- )=-
)=- ,
,故答案为:
 或-
或- .
.点评:此题主要考查了直线与圆的位置关系,解决问题的关键是根据题意确定出P点的坐标.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
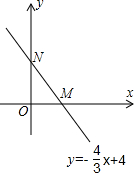 如图,直线y=-
如图,直线y=-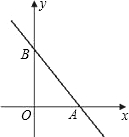 如果点P在坐标轴上,以点P为圆心,
如果点P在坐标轴上,以点P为圆心,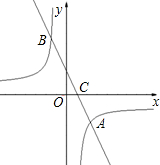 C,如果点D在坐标轴上,且OA=DC.
C,如果点D在坐标轴上,且OA=DC.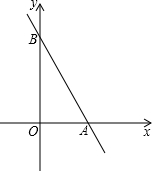 如果点P在坐标轴上,以P为圆心,
如果点P在坐标轴上,以P为圆心,