题目内容
 如图,正比例函数y=kx(k≠0)的图象与反比例函数y=
如图,正比例函数y=kx(k≠0)的图象与反比例函数y=| m |
| x |
| 4 |
| 5 |
求(1)求反比例函数与正比例函数的解析式;
(2)求△ANB的面积.
分析:(1)根据cos∠AOC=
设OC=4x,AO=5x,再利用勾股定理算出AC=3x,然后根据△AOC的面积是24,求出x的值,进而得到A点坐标,再利用待定系数法求出反比例函数与正比例函数的解析式;
(2)A、B两点是反比例函数与正比例函数的交点,故A、B两点关于原点对称,根据A点坐标得到B点坐标,△ANB的面积可以表示为S△BNO+S△AON,再利用三角形的面积公式代入相应数值进行计算即可.
| 4 |
| 5 |
(2)A、B两点是反比例函数与正比例函数的交点,故A、B两点关于原点对称,根据A点坐标得到B点坐标,△ANB的面积可以表示为S△BNO+S△AON,再利用三角形的面积公式代入相应数值进行计算即可.
解答:解:(1)∵cos∠AOC=
,
∴设OC=4x,AO=5x,
则AC=
=3x,
∵△AOC的面积是24,
∴
•CA•CO=24,
×3x×4x=24,
解得:x=±2,
∵A在第四象限,
∴A(8,-6)
把A(8,-6)代入正比例函数y=kx中得;k=-
,
则正比例函数解析式为:y=-
x,
把A(8,-6)代入反比例函数y=
中得;m=-48,
则反比例函数解析式为:y=-
;
(2)∵A、B两点是反比例函数与正比例函数的交点,A(8,-6),
∴B(-8,6),
∵点N的坐标是(-5,0),
∴NO=5,
∴S△BNA=S△BNO+S△AON=
×5×6+
×5×6=30.
| 4 |
| 5 |
∴设OC=4x,AO=5x,
则AC=
| AO2-OC2 |
∵△AOC的面积是24,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得:x=±2,
∵A在第四象限,
∴A(8,-6)
把A(8,-6)代入正比例函数y=kx中得;k=-
| 3 |
| 4 |
则正比例函数解析式为:y=-
| 3 |
| 4 |
把A(8,-6)代入反比例函数y=
| m |
| x |

则反比例函数解析式为:y=-
| 48 |
| x |
(2)∵A、B两点是反比例函数与正比例函数的交点,A(8,-6),
∴B(-8,6),
∵点N的坐标是(-5,0),
∴NO=5,
∴S△BNA=S△BNO+S△AON=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了三角函数的应用,待定系数法求出函数解析式,以及三角形面积的求法,解决此题的关键是根据三角形的面积结合三角函数求出A点坐标.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
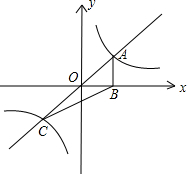 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y=| 1 |
| x |
| A、S=1 | B、S=2 |
| C、S=3 | D、S的值不能确定 |
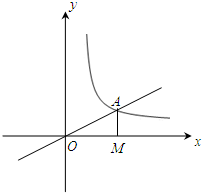 如图,正比例函数
如图,正比例函数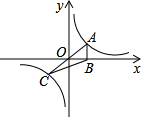 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y= 作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点.
作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点. 已知:如图,正比例函数y=k1x的图象与反比例函数
已知:如图,正比例函数y=k1x的图象与反比例函数