题目内容
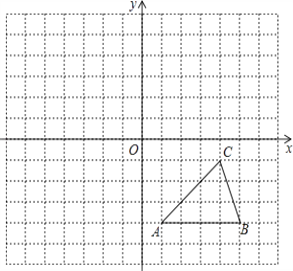
【题目】如图1,在平面直角坐标系中,![]() ,
,![]() 是
是![]() 轴正半轴上一点,
轴正半轴上一点,![]() ,若
,若![]() 与
与![]() 互为相反数.
互为相反数.


(1)求![]() 的值;
的值;
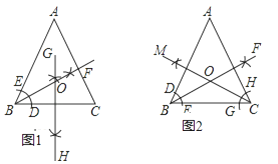
(2)如图2,![]() 交
交![]() 轴于
轴于![]() ,以
,以![]() 为边的正方形
为边的正方形![]() 的对角线
的对角线![]() 交
交![]() 轴于
轴于![]() .
.
①求证:![]() ;
;
②记![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)①见解析,②3
;(2)①见解析,②3
【解析】
(1)根据相反数的概念得出方程![]() ,求出
,求出![]() 的值,作AG⊥OB于G,利用含30度角的直角三角形的性质即可求得答案;
的值,作AG⊥OB于G,利用含30度角的直角三角形的性质即可求得答案;
(2)①延长AC交y轴于点Q,作AP⊥OA交OB于P,利用“ASA”证得△OAQ![]() △PAB,得到AQ= AB,
△PAB,得到AQ= AB,![]() ,QC=2OC,再利用线段的和差即可证明;
,QC=2OC,再利用线段的和差即可证明;
②连接QF,利用“SAS”证得△FAQ![]() △FAB,得到
△FAB,得到![]() ,从而证得结论.
,从而证得结论.
(1)∵![]() 和
和![]() 互为相反数,
互为相反数,
∴![]() ,
,
∴![]() ,
,![]()
![]() ,
,
∴![]() ,
,
如图:作AG⊥OB于G,
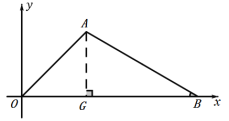
∵点A的坐标为(![]() ,
,![]() ),即A (
),即A (![]() ,
,![]() ),
),
∴AG=OG=2,
在Rt![]() BAG中,∠ABG=30
BAG中,∠ABG=30![]() ,AG=2,
,AG=2,
∴AB=2AG=4,
BG=![]() ,
,
∴BO= OG+ BG=2+![]() ,
,
∴![]() ;
;
(2)①延长AC交![]() 轴于点Q,作AP⊥OA交OB于P,如图:
轴于点Q,作AP⊥OA交OB于P,如图:
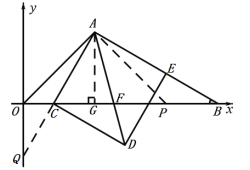
由(1)得AG=OG=2,AG⊥OB,
∴∠AOG=45![]() ,
,
∵AP⊥OA,
∴∠APO=90![]() -∠AOG =45
-∠AOG =45![]() ,
,
∴∠APO=∠AOG=45![]() ,
,
∴AO=AP,∠APB=180![]() -45
-45![]() =135
=135![]() ,
,
∠AOQ=90![]() +45
+45![]() =135
=135![]() ,
,
∴∠APB=∠AOQ,
∵AP⊥OA,AC⊥AB,
∴∠OAP=∠CAB=90![]() ,
,
∴∠OAQ+∠CAP =∠PAB+∠CAP =90![]() ,
,
∴∠OAQ=∠PAB,
在△OAQ和△PAB中,
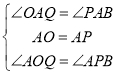 ,
,
∴△OAQ![]() △PAB(ASA),
△PAB(ASA),
∴AQ= AB,![]() ,
,
在Rt![]() OQC中,∠OQC=30
OQC中,∠OQC=30![]() ,
,
∴QC=2OC,
∵四边形ACDE为正方形,
∴AC=AE,
∴BE=AB-AE=AQ-AC=QC=2OC;
②如图,连接QF,
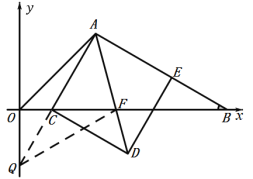
∵四边形ACDE为正方形,AD为对角线,
∴![]() ,
,
由①得:AQ= AB,![]() ,QC=2OC,
,QC=2OC,
∴![]() ,
,
在△FAQ和△FAB中,
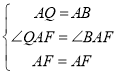 ,
,
∴△FAQ![]() △FAB (SAS),
△FAB (SAS),
∴QF=BF,
∴![]() ,
,
∴![]() .
.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案