��Ŀ����
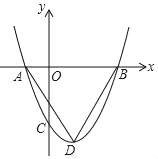
����Ŀ����֪��ͼ��ֱ��AB��x���ڵ�A����y���ڵ�B��AB��![]() ��tan��BAO��3��
��tan��BAO��3��
��1����ֱ��AB�Ľ���ʽ��
��2��ֱ��y��kx+b������B��x�ύ�ڵ�C���ҡ�ABC��45�㣬AD��BC�ڵ�D������P�ӵ�C��������CB������ÿ��![]() ����λ���ȵ��ٶ����յ�B�˶����˶�ʱ��Ϊt�����ADP�����ΪS����S��t�ĺ�����ϵʽ����ֱ��д���Ա���t��ȡֵ��Χ��
����λ���ȵ��ٶ����յ�B�˶����˶�ʱ��Ϊt�����ADP�����ΪS����S��t�ĺ�����ϵʽ����ֱ��д���Ա���t��ȡֵ��Χ��
��3���ڣ�2���������£���P���߶�BD�ϣ���F���߶�AB�ϣ���APC����FPB������AP������F��FG��AP�ڵ�G����AD�ڵ�H����DP��DH�����P�����꣮
���𰸡���1��y��3x+6����2����0��t��1ʱ��S��5��5x����1��t��3ʱ��S��5x��5����3����P��![]() ��
��![]() ��
��
��������
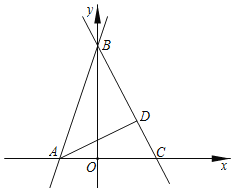
��1�������Ǻ������ɶ��������A����B���꣬�ô���ϵ�����������ʽ��
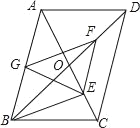
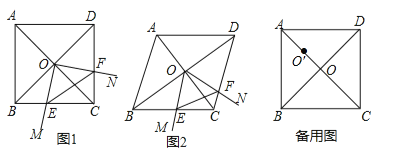
��2����ͼ1������D��EF��AC����AC�ڵ�F������B��BE��EF������ΪE���ɡ�AAS����֤��BDE�ա�DAF���ɵ�DF��BE��DE��AF�������D���꣬����BC����ʽ���ɹ��ɶ�������BC�ij����������ʽ����⣻
��3����ͼ2������B��BN��AB��AP�ӳ�����N���ɡ�ASA����֤��BPN�ա�BPF���ɵ�BN��BF��PN��PF���ɡ�AAS����֤��AHF�ա�BPN���ɵ�AF��BN��PN��FH�������F���꣬��������빫ʽ����BF��![]() ��BN��ͨ��֤����MNP�ס�DAP���ɵ�
��BN��ͨ��֤����MNP�ס�DAP���ɵ�![]() ������PD�ij�����������빫ʽ�����P���꣮
������PD�ij�����������빫ʽ�����P���꣮
�⣺��1����tan��BAO��3��![]() ��
��
��BO��3AO��
��AB2��AO2+BO2��40��
��AO��2��BO��6��
���A����2��0������B��0��6��
��ֱ��AB����ʽΪ��y��kx+6��
��0����2k+6��
��k��3��
��ֱ��AB����ʽΪ��y��3x+6��
��2����ͼ1������D��EF��AC����AC�ڵ�F������B��BE��EF������ΪE��
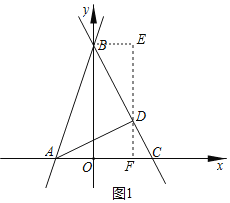
���ı���BEFO�Ǿ��Σ�
��BO��EF��6��OF��BE��
�ߡ�ABC��45�㣬AD��BC��
���ABC����BAD��45�㣬
��AD��BD��
�ߡ�ADB��90�㣽��AFD��
���BDE+��ADF��90�㣬��ADF+��DAF��90�㣬
���BDE����DAF����BD��AD����E����AFD��90�㣬
���BDE�ա�DAF��AAS��
��DF��BE��DE��AF��
��EF��ED+DF��AO+OF+OF��2+2OF��6
��OF��2��
���D���꣨2��2����
��BC����ʽΪ��y��ax+6��
��2��2a+6��
��a����2��
��ֱ��BC����ʽΪ��y����2x+6��
�൱y��0ʱ��x��3��
���C��3��0����
��OC��3��
��BC��![]() ��3
��3![]() ��
��
��AB��2![]() ���ҡ�ABC��45�㣬AD��BC��
���ҡ�ABC��45�㣬AD��BC��
��AD��BD��2![]() ��
��
��CD��![]() ��
��
��0��t��1ʱ��S��![]() ��2
��2![]() ����
����![]() ��
��![]() x����5��5x��
x����5��5x��
��1��t��3ʱ��S��![]() ��2
��2![]() ����
����![]() x��
x��![]() ����5x��5��
����5x��5��
��3����ͼ2������B��BN��AB��AP�ӳ�����N������N��MN��BC��M��
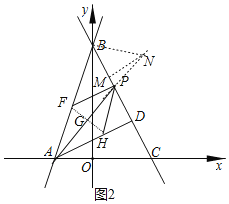
��AD��BD��DH��PD��
��AH��BP��
��BN��AB����ABC��45�㣬
���ABC����NBP��45�㣬�ҡ�APC����BPN����BPF��BP��BP��
���BPN�ա�BPF��ASA��
��BN��BF��PN��PF��
��FH��AP��
���AGF����ABN��90�㣬
���FAG+��AFG��90�㣬��FAG+��N��90�㣬
���AFG����N���ҡ�BAD����PBN��45�㣬AH��BP��
���AHF�ա�BPN��AAS��
��AF��BN��PN��FH��
��BF��AF��FH��FP��
���F��AB�е㣬
���F���꣨��1��3��
��BF��![]() ��BN��
��BN��
�ߡ�NBM��45�㣬
��BM��MN��![]() ��
��
��MD��BD��BM��![]() ��
��
��MN��BC��AD��BC��
��AD��MN��
���MNP�ס�DAP��
��![]()
��![]() ����MP+PD��
����MP+PD��![]()
��PD��![]()
���P��x����2x+6����
�ࣨx��2��2+����2x+6��2��2��![]() ��
��
��x��![]() ��x��
��x��![]() ������������ȥ��
������������ȥ��
���P��![]() ��
��![]() ��
��

����Ŀ����һ�������Ŀڴ���װ�����ɸ��ʵ���ͬ�ĺ���Ϊ�˹��ƴ��к����������ijѧϰС�������������飬���ǽ�30��������С��״��ȫ��ͬ�İ���װ����У����Ⱥ�����������1��������ɫ���ٰ����Żش��У�����ظ������±��Ƕ������������ܺ�ͳ�Ƶ����ݣ�
����Ĵ��� | 150 | 200 | 500 | 900 | 1 000 | 1 200 |
���������Ƶ�� | 51 | 64 | 156 | 275 | 303 | 361 |
���������Ƶ�� | 0.320 | 0.312 | 0.306 | 0.303 | 0.302 | 0.301 |
(1)����ƣ�������Ĵ����ܴ�ʱ�����������Ƶ�ʽ���ӽ�______��������ȥ��һ�Σ������������ĸ�����______��(��ȷ��0.1)
(2)�Թ��ƿڴ��к����ж��ٸ���