题目内容
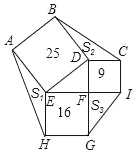
【题目】![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 为线段
为线段![]() 上一点(
上一点(![]() 点不和
点不和![]() 两点重合),连接
两点重合),连接![]() 并延长
并延长![]() ,在
,在![]() 的延长线上找一点
的延长线上找一点![]() ,使
,使![]() .点
.点![]() 为线段
为线段![]() 上一点(
上一点(![]() 点不和
点不和![]() 两点重合),连接
两点重合),连接![]() ,交
,交![]() 于点
于点![]() .
.
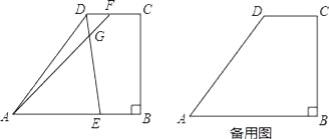
(1)如图1,若![]() 是线段
是线段![]() 的中点,求
的中点,求![]() .
.
(2)如图2,若点![]() 是线段
是线段![]() 的中点,
的中点,![]() ,求证:
,求证:![]() .
.

【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据等腰直角三角形的性质得到![]() ,根据勾股定理得到
,根据勾股定理得到![]() 根据线段的中点的定义得到
根据线段的中点的定义得到![]() ,由勾股定理得到结论;
,由勾股定理得到结论;
(2)过A作AH∥CD交BD于H,得到∠AHD=∠CDH,根据全等三角形的性质得到DE=EH,AH=CD,推出四边形AHCD是矩形,得到∠HAD=90°,根据全等三角形的性质得到BH=CF,由线段的和差得到结论.
解:(1)∵△ABC是等腰直角三角形,![]()
![]()
∵AD⊥CD,
∴∠ADC=90°,
∵CD=1,
∴![]()
∵F是线段AD的中点,
∴![]()
![]()
(2)过A作AH∥CD交BD于H,
∴∠AHD=∠CDH,
∵点E是线段AC中点,
∴AE=CE,
在△AEH与△CED中,
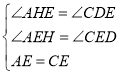
∴△AEH≌△CED(AAS),
∴DE=EH,AE=CE,
∴四边形AHCD是平行四边形,
∵∠ADC=90°,
∴四边形AHCD是矩形,
∴∠HAD=90°,
∵∠BAC=90°,
∴∠BAH=∠FAC,
∵DE⊥CF,
∴∠DFG=∠CDG,
∴∠AHE=∠DFG,
∴∠AHB=∠AFC,
在△ABH与△ACF中
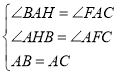
∴△ABH≌△ACF(AAS),
∴BH=CF,
∵BE=BH+EH,
∴CF+DE=BE.


【题目】我们知道不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式组是否也具有类似的性质呢?请解答下列问题.
(1)完成下列填空:
已知 | 用“<”或“>”填空 |
| 5+2_____3+1 |
| ﹣3﹣1_____﹣5﹣2 |
| 1﹣2_____4+1 |
(2)一般地,如果![]() 那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.