题目内容
13. 如图所示,已知△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE.
如图所示,已知△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE.(1)求证:△ABC≌△ADE;
(2)若∠3=∠C,求证:AE∥BC.
分析 (1)求出∠BAC=∠DAE,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠B=∠ADE,然后利用“角角边”证明△ABC和△ADE全等即可;
(2)根据全等三角形对应角相等可得∠E=∠C,从而可以求出∠E=∠3,然后根据内错角相等,两直线平行证明即可.
解答 证明:(1)∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
即∠BAC=∠DAE,
由三角形的外角性质得,∠B+∠1=∠ADE+∠3,
∵∠1=∠3,
∴∠B=∠ADE,
在△ABC和△ADE中,$\left\{\begin{array}{l}{∠BAC=∠DAE}\\{∠B=∠ADE}\\{AC=AE}\end{array}\right.$,
∴△ABC≌△ADE(AAS);
(2)∵△ABC≌△ADE,
∴∠E=∠C,
∵∠3=∠C,
∴∠E=∠3,
∴AE∥BC.
点评 本题考查了全等三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,平行线的判定,熟练掌握三角形全等的判定方法是解题的关键.

练习册系列答案
相关题目
3.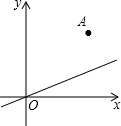 如图,已知点A(1,1)关于直线y=kx的对称点恰好落在x轴的正半轴上,则k的值是( )
如图,已知点A(1,1)关于直线y=kx的对称点恰好落在x轴的正半轴上,则k的值是( )
 如图,已知点A(1,1)关于直线y=kx的对称点恰好落在x轴的正半轴上,则k的值是( )
如图,已知点A(1,1)关于直线y=kx的对称点恰好落在x轴的正半轴上,则k的值是( )| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$-1 | C. | 2-$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
1.水库管理人员为掌握水库蓄水情况,需要观测水库水位变化,如表是一周内水位高低的变化情况,用正数表示水位比前一天上升数,用负数表示水位比前一天下降数.
(1)问水库的水位在本周内是上升还是下降,幅度是多少?
(2)这一周内,哪一天水库的水位最高?哪一天的水位最低?最高水位比最低水位高多少?
| 星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 水位变化(cm) | 10 | -1 | -12 | 6 | -20 | -5 | 30 |
(2)这一周内,哪一天水库的水位最高?哪一天的水位最低?最高水位比最低水位高多少?
 已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AC=10cm,则矩形的面积为25$\sqrt{3}$cm2.
已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AC=10cm,则矩形的面积为25$\sqrt{3}$cm2.