题目内容
锐角三角形ABC的三边长满足不等式AB＜AC＜BC，如果I为△ABC的内心，O为外心，求证：直线IO与线段AB及BC相交．
解：连接AO、CO并延长分别交对边于D、E，
∵∠AOC=2∠B，
∴∠OAC=90°-∠B＜90°-∠C（∠A＞∠B＞∠C），
但90°-∠B+90°-∠C=∠A，从而∠OAC＜
∠A，
即I在∠BAD内部．
又∵∠ACO=90°-∠B＞90°-∠A，
同理有∠OCA＞∠C．
∴I在∠ACE内部，即I在△AOE内，
从而IO与线段AB及BC相交．
分析：连接AO、CO并延长分别交对边于D、E，先证I在△AOE内，从而直线IO与线段AE及CD相交．
点评：本题考查了三角形的内切圆和外接圆，是基础知识要熟练掌握．
∵∠AOC=2∠B，
∴∠OAC=90°-∠B＜90°-∠C（∠A＞∠B＞∠C），
但90°-∠B+90°-∠C=∠A，从而∠OAC＜
∠A，即I在∠BAD内部．
又∵∠ACO=90°-∠B＞90°-∠A，
同理有∠OCA＞
∠C．∴I在∠ACE内部，即I在△AOE内，
从而IO与线段AB及BC相交．
分析：连接AO、CO并延长分别交对边于D、E，先证I在△AOE内，从而直线IO与线段AE及CD相交．
点评：本题考查了三角形的内切圆和外接圆，是基础知识要熟练掌握．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
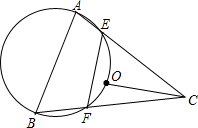OC，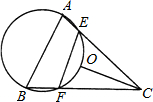
如图，已知点O是锐角三角形ABC的外心，过A、B、O三点的圆交于AC、BC于E、F，且EF=OC．