题目内容
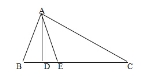
(本题满分12分)如图,在△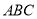 中,∠
中,∠ >∠
>∠ ,
,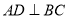 ,
,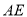 平分∠
平分∠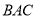 .
.
(1)若∠ =70°,∠
=70°,∠ =30°.
=30°.
①求∠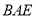 = °;②∠
= °;②∠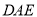 = °.
= °.
(2)探究:小明认为如果只要知道∠ -∠
-∠ =n°,就能求出∠
=n°,就能求出∠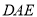 的度数?请你就这个问题展开探究:
的度数?请你就这个问题展开探究:
①实验:填表
∠ | ∠ | ∠ |
70° | 30° | (此格不需填写) |
65° | 25° | |
50° | 20° | |
80° | 56° |
②结论:当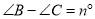 时,试用含
时,试用含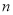 的代数式表示∠
的代数式表示∠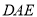 的度数,并写出推导过程;
的度数,并写出推导过程;
③应用:若∠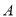 =56°,∠
=56°,∠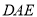 =12°,则∠
=12°,则∠ = °
= °
(1)①40°;②20°;(2)见解析;(3)74°.
【解析】
试题分析:(1)根据△ABC的内角和求出∠BAC的度数,然后根据角平分线的性质求出∠BAE的度数,根据△ABD的内角和求出∠BAD的度数,然后计算∠DAE的度数;(2)同(1)的方法进行填表;根据三角形内角和以及角平分线的性质将∠BAE的度数用含有∠B和∠C的式子表示,根据△ABD的内角和将∠BAD用含∠B的式子表示,然后根据∠DAE=∠BAE-∠BAD进行计算;(3)根据得出的规律进行计算.
试题解析:(1)①40°; ②20°;
(2)①填表
∠ | ∠ | ∠ |
70° | 30° | (此格不需填写) |
65° | 25° | 20° |
50° | 20° | 15° |
80° | 56° | 12° |
②【解析】
在△ABC中,∠BAC=180°-∠B-∠C.
∵AE平分∠BAC,∴∠BAE=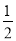 ∠BAC=
∠BAC=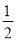 (18O°-∠B-∠C). =90°-
(18O°-∠B-∠C). =90°-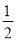 ∠B-
∠B-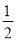 ∠C.
∠C.
∵AD⊥BC, ∴∠ADB=90°. ∴∠BAD+∠B=90°. ∴ ∠BAD=90°-∠B
∴ ∠DAE=∠BAE-∠BAD =(90°-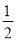 ∠B-
∠B-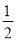 ∠C)-(90°-∠B)=
∠C)-(90°-∠B)=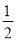 ∠B-
∠B-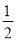 ∠C=
∠C= (∠B-∠C)=
(∠B-∠C)= n°;
n°;
③ 74°.
考点:三角形内角和定理、角平分线的性质.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案 的度数
的度数 的度数
的度数 的度数
的度数 .
. C、
C、 D、
D、
 +3,当x 时,函数值y随x的增大而增大。
+3,当x 时,函数值y随x的增大而增大。 =80 (D)60
=80 (D)60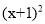 =80
=80

 在实数范围内有意义,则
在实数范围内有意义,则 的取值范围是 .
的取值范围是 .