题目内容
 如图,△ABC为等边三角形,DC∥AB,AD⊥CD于D.若△ABC的周长为12cm,则CD=
如图,△ABC为等边三角形,DC∥AB,AD⊥CD于D.若△ABC的周长为12cm,则CD=考点:含30度角的直角三角形,等边三角形的性质
专题:
分析:根据等边三角形的性质求出AC,∠BAC=60°,再根据两直线平行,内错角相等可得∠ACD=∠BAC,然后根据直角三角形两锐角互余求出∠CAD=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得CD=
AC.
| 1 |
| 2 |
解答:解:∵△ABC为等边三角形,
∴AC=12÷3=4,∠BAC=60°,
∵DC∥AB,
∴∠ACD=∠BAC=60°,
∵AD⊥CD,
∴∠CAD=90°-60°=30°,
∴CD=
AC=
×4=2cm.
故答案为:2.
∴AC=12÷3=4,∠BAC=60°,
∵DC∥AB,
∴∠ACD=∠BAC=60°,
∵AD⊥CD,
∴∠CAD=90°-60°=30°,
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:2.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,等边三角形的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
多项式-
+3x+27的次数是( )
| 3xy4 |
| 4 |
| A、7 | B、5 | C、6 | D、13 |
下列运算中正确的是( )
| A、x3•x3=2x6 |
| B、(-x3)2=-x6 |
| C、x5+x=x6 |
| D、(5x)3=125x3 |
下列结论中正确的是( )
| A、有两边及一角对应相等的两个三角形全等 |
| B、有两角及一边相等的两个三角形全等 |
| C、有两边相等的两个直角三角形全等 |
| D、有斜边和一锐角相等的两个直角三角形全等 |
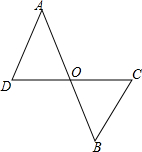 如图所示,AB、CD相交于点O,已知OA=OB,请补充一个条件使得△AOD≌△BOC,你补充的条件是
如图所示,AB、CD相交于点O,已知OA=OB,请补充一个条件使得△AOD≌△BOC,你补充的条件是 如图,在平面直角坐标系xOy中,A(4,4)、B(1,2)、C(3,2).若△ABC与△DBC全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(4,4)、B(1,2)、C(3,2).若△ABC与△DBC全等,则点D坐标为