ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΙψΈςΓΑΒΨ”ψΉέΚœ―χ÷≥Γ±ΖϊΚœ…ζΧ§―χ÷≥Θ§¬Χ…ΪΖΔ’ΙΘ°Ρ≥ΒΨ”ψΉέΚœ―χ÷≥ΜßΦΤΜ°ΙΚ¬ρΦΉΘ§““ΝΫ÷÷ΚΧΜ®”ψ”ψΟγΘ§Ψ≠Βς≤ιΘ§ΒΟΒΫ“‘œ¬–≈œΔΘΚ
ΙΚ¬ρ÷ΊΝΩ–Γ”Ύ40 kg | ΙΚ¬ρ÷ΊΝΩ≤Μ–Γ”Ύ40 kg | |
ΦΉ”ψΟγ | ‘≠Φέœζ έ | ¥ρΤΏ’έœζ έ |
““”ψΟγ | ‘≠Φέœζ έ | ¥ρΑΥ’έœζ έ |
»γΙϊΙΚ¬ρ10 kgΒΡΦΉ”ψΟγΚΆ5 kgΒΡ““”ψΟγ–η”Ο700‘ΣΘ§»γΙϊΙΚ¬ρ20 kgΒΡΦΉ”ψΟγΚΆ15 kgΒΡ““”ψΟγ–η”Ο1600‘ΣΘ°
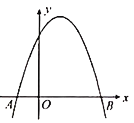
Θ®1Θ©ΦΉ”ψΟγΚΆ““”ψΟγΒΡΒΞΦέΗς «Εύ…Ό‘ΣΘΩ
Θ®2Θ©œ÷ΨωΕ®ΙΚ¬ρΦΉΘ§““ΝΫ÷÷”ψΜΤΙ≤90 kgΘ§Τδ÷–Θ§““”ψΟγΒΡ÷ΊΝΩ≤Μ¥σ”ΎΦΉ”ψΟγ÷ΊΝΩΒΡ2±ΕΘ§…ηΙΚ¬ρΦΉ”ψΟγa kgΘ®![]() Θ©Θ§«σΗΟ―χ÷≥ΜßΙΚ¬ρ’β≈ζ”ψΟγΒΡΉήΖ―”ΟW”κa÷°ΦδΒΡΚ· ΐΫβΈω ΫΘΜ
Θ©Θ§«σΗΟ―χ÷≥ΜßΙΚ¬ρ’β≈ζ”ψΟγΒΡΉήΖ―”ΟW”κa÷°ΦδΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§«κ…ηΦΤ“Μ÷÷ΙΚ¬ρΖΫΑΗΘ§ ΙΥυ–ηΉήΖ―”ΟΉνΒΆΘ§≤Δ«σ≥ωΉνΒΆΉήΖ―”ΟΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦΉ”ψΟγΦέΗώΈΣ50‘Σ/kgΘ§““”ψΟγΦέΗώΈΣ40‘Σ/kgΘΜΘ®2Θ©ΔΌΒ±![]() ±Θ§
±Θ§ ![]() ΘΜΔΎΒ±
ΘΜΔΎΒ±![]() ±Θ§
±Θ§ ![]() ΘΜΘ®3Θ©Β±ΙΚ¬ρΦΉ”ψΟγ40 kgΘ§““”ψΟγ50 kg ±Θ§Υυ–ηΉήΖ―”ΟΉνΒΆΘ§ΉνΒΆΉήΖ―”ΟΈΣ3000‘Σ
ΘΜΘ®3Θ©Β±ΙΚ¬ρΦΉ”ψΟγ40 kgΘ§““”ψΟγ50 kg ±Θ§Υυ–ηΉήΖ―”ΟΉνΒΆΘ§ΉνΒΆΉήΖ―”ΟΈΣ3000‘Σ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧβ“βΝ–Εΰ‘Σ“Μ¥ΈΖΫ≥ΧΉιΫχ––Ϋβ¥πΘΜ
Θ®2Θ©ΗυΨίΝΫ÷÷”ψΟγ÷ΊΝΩ÷°ΦδΒΡΙΊœΒΘ§Ν–≥ω≤ΜΒ» ΫΘ®ΉιΘ©«σ≥ωΙΚ¬ρΦΉ”ψΟγ÷ΊΝΩaΒΡ»Γ÷ΒΖΕΈßΘ§‘Ό“άΨίaΒΡ»Γ÷ΒΖΕΈßΖ÷ΕΈΩΦ¬«ΉήΖ―”ΟW”κaΒΡΙΊœΒ ΫΘΜ
Θ®3Θ©ΗυΨί“Μ¥ΈΚ· ΐΒΡ–‘÷ Θ§Ζ÷ΕΈΧ÷¬έΘ§»ΖΕ®Β±a»ΓΚΈ÷Β ±Θ§Ζ―”ΟWΉνΒΆΘ§ΉνΚσΉέΚœ»ΖΕ®Ζ―”ΟWΉνΒΆ ±ΒΡΙΚ¬ρΖΫΑΗΘ°
ΫβΘΚΘ®1Θ©…ηΦΉ”ψΟγΦέΗώΈΣx‘Σ/kgΘ§““”ψΟγΦέΗώΈΣy‘Σ/kgΘ§
”…Χβ“βΒΟ![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§
¥πΘΚΦΉ”ψΟγΦέΗώΈΣ50‘Σ/kgΘ§““”ψΟγΦέΗώΈΣ40‘Σ/kgΘΜ
Θ®2Θ©ΗυΨίΧβ“βΒΟΘΚ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΔΌΒ±![]() ±Θ§
±Θ§
WΙΊ”ΎaΒΡΫβΈω ΫΈΣΘΚ![]() ΘΜ
ΘΜ
ΔΎΒ±![]() ±Θ§WΙΊ”ΎaΒΡΫβΈω ΫΈΣΘΚ
±Θ§WΙΊ”ΎaΒΡΫβΈω ΫΈΣΘΚ
![]() ΘΜ
ΘΜ
Θ®3Θ©ΔΌΒ±![]() ±Θ§
±Θ§![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
ΓύWΥφaΒΡ‘ω¥σΕχ‘ω¥σΘ§
ΓύΒ±![]() ±Θ§WΒΡ÷ΒΉν–ΓΘ§¥Υ ±
±Θ§WΒΡ÷ΒΉν–ΓΘ§¥Υ ±![]() Θ®‘ΣΘ©ΘΜ
Θ®‘ΣΘ©ΘΜ
ΔΎΒ±![]() ±Θ§
±Θ§![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
ΓύWΥφaΒΡ‘ω¥σΕχ‘ω¥σΘ§
ΓύΒ±![]() ±Θ§WΒΡ÷ΒΉν–ΓΘ§¥Υ ±
±Θ§WΒΡ÷ΒΉν–ΓΘ§¥Υ ±![]() Θ®‘ΣΘ©Θ§
Θ®‘ΣΘ©Θ§
ΓΏ![]() Θ§
Θ§
ΓύΒ±ΙΚ¬ρΦΉ”ψΟγ40 kgΘ§““”ψΟγ50 kg ±Θ§Υυ–ηΉήΖ―”ΟΉνΒΆΘ§ΉνΒΆΉήΖ―”ΟΈΣ3000‘Σ.

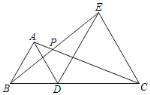
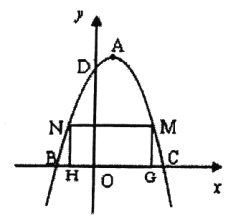
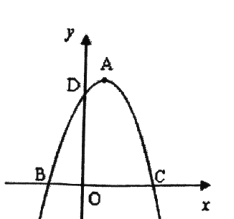
ΓΨΧβΡΩΓΩΡ≥ –ΨΌ––÷Σ Ε¥σ»ϋΘ§A–ΘΓΔB–ΘΗς≈…≥ω5Οϊ―Γ ÷Ήι≥…¥ζ±μΕ”≤ΈΦ”Ψω»ϋΘ§ΝΫ–Θ≈…≥ω―Γ ÷ΒΡΨω»ϋ≥…Φ®»γΆΦΥυ ΨΘ°
![]() ΗυΨίΆΦ ΨΧν–¥œ¬±μΘΚ
ΗυΨίΆΦ ΨΧν–¥œ¬±μΘΚ
ΤΫΨυ ΐ | ÷–ΈΜ ΐ | ÷Ύ ΐ | |
A–Θ | ______ | 85 | ______ |
B–Θ | 85 | ______ | 100 |
![]() ΫαΚœΝΫ–Θ≥…Φ®ΒΡΤΫΨυ ΐΚΆ÷–ΈΜ ΐΘ§Ζ÷ΈωΡΡΗω―ß–ΘΒΡΨω»ϋ≥…Φ®ΫœΚΟΘΜ
ΫαΚœΝΫ–Θ≥…Φ®ΒΡΤΫΨυ ΐΚΆ÷–ΈΜ ΐΘ§Ζ÷ΈωΡΡΗω―ß–ΘΒΡΨω»ϋ≥…Φ®ΫœΚΟΘΜ
![]() ΦΤΥψΝΫ–ΘΨω»ϋ≥…Φ®ΒΡΖΫ≤νΘ§≤Δ≈–ΕœΡΡΗω―ß–Θ¥ζ±μΕ”―Γ ÷≥…Φ®ΫœΈΣΈ»Ε®Θ°
ΦΤΥψΝΫ–ΘΨω»ϋ≥…Φ®ΒΡΖΫ≤νΘ§≤Δ≈–ΕœΡΡΗω―ß–Θ¥ζ±μΕ”―Γ ÷≥…Φ®ΫœΈΣΈ»Ε®Θ°