题目内容
 如图,已知在矩形ABCD中,AB=6,BC=8,⊙E和⊙F分别是△ABC和△ADC的内切圆,与对角线AC分别切于E、F,则EF=________.
如图,已知在矩形ABCD中,AB=6,BC=8,⊙E和⊙F分别是△ABC和△ADC的内切圆,与对角线AC分别切于E、F,则EF=________.
2
分析:连接EM、EN、EQ、AE、BE、CE、过F作FW⊥BC于W,过E作ER⊥FW于R,根据三角形的面积公式求出⊙E和⊙F的半径,在Rt△EFR中,根据勾股定理求出即可.
解答:
连接EM、EN、EQ、AE、BE、CE、过F作FW⊥BC于W,过E作ER⊥FW于R,
设⊙E的半径是R,
则EM=EN=EQ=RW=R,
∵四边形ABCD是矩形,
∴AB=CD=6,AD=BC=8,∠ABC=90°,
在Rt△ABC中,AB=6,BC=8,由勾股定理得:AC=10,
∵S△ABE+S△BCE+S△ACE=S△ABC,
∴ ×6×R+
×6×R+ ×8×R+
×8×R+ ×10×R=
×10×R= ×6×8,
×6×8,
R=2,
同法可求出⊙F的半径是2,
在Rt△EFR中,ER=8-2-2=4,FR=6-2-2=2,由勾股定理得:EF= =2
=2 ,
,
故答案为:2 .
.
点评:本题考查了三角形的内切圆和内心,三角形的面积公式,切线的性质,勾股定理,矩形的性质等知识点的综合应用,主要考查学生的推理能力和计算能力.

分析:连接EM、EN、EQ、AE、BE、CE、过F作FW⊥BC于W,过E作ER⊥FW于R,根据三角形的面积公式求出⊙E和⊙F的半径,在Rt△EFR中,根据勾股定理求出即可.
解答:

连接EM、EN、EQ、AE、BE、CE、过F作FW⊥BC于W,过E作ER⊥FW于R,
设⊙E的半径是R,
则EM=EN=EQ=RW=R,
∵四边形ABCD是矩形,
∴AB=CD=6,AD=BC=8,∠ABC=90°,
在Rt△ABC中,AB=6,BC=8,由勾股定理得:AC=10,
∵S△ABE+S△BCE+S△ACE=S△ABC,
∴
 ×6×R+
×6×R+ ×8×R+
×8×R+ ×10×R=
×10×R= ×6×8,
×6×8,R=2,
同法可求出⊙F的半径是2,
在Rt△EFR中,ER=8-2-2=4,FR=6-2-2=2,由勾股定理得:EF=
 =2
=2 ,
,故答案为:2
 .
.点评:本题考查了三角形的内切圆和内心,三角形的面积公式,切线的性质,勾股定理,矩形的性质等知识点的综合应用,主要考查学生的推理能力和计算能力.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
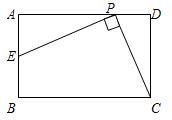 自选题:
自选题: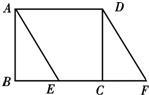 如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.
如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.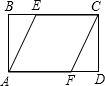 如图,已知在矩形ABCD中,AB=2,BC=4,四边形AFCE为菱形,求菱形的面积.
如图,已知在矩形ABCD中,AB=2,BC=4,四边形AFCE为菱形,求菱形的面积. 如图,已知在矩形ABCD中,AB=6,BC=8,⊙E和⊙F分别是△ABC和△ADC的内切圆,与对角线AC分别切于E、F,则EF=
如图,已知在矩形ABCD中,AB=6,BC=8,⊙E和⊙F分别是△ABC和△ADC的内切圆,与对角线AC分别切于E、F,则EF=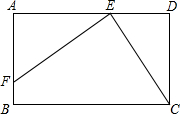 E=3cm,BC=7cm.
E=3cm,BC=7cm.