题目内容
19.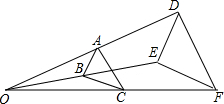 如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的$\frac{4}{9}$,则AB:DE=2:3.
如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的$\frac{4}{9}$,则AB:DE=2:3.
分析 由△ABC经过位似变换得到△DEF,点O是位似中心,根据位似图形的性质,即可得AB∥DE,即可求得△ABC的面积:△DEF面积=$\frac{4}{9}$,得到AB:DE═2:3.
解答 解:∵△ABC与△DEF位似,位似中心为点O,
∴△ABC∽△DEF,
∴△ABC的面积:△DEF面积=($\frac{AB}{DE}$)2=$\frac{4}{9}$,
∴AB:DE=2:3,
故答案为:2:3.
点评 此题考查了位似图形的性质.注意掌握位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方.

练习册系列答案
相关题目
9.为了解峨边今年参加中考的1000名学生的体重情况,抽查了其中200名学生的体重进行统计分析,下列叙述正确的是( )
| A. | 200名学生是总体 | |
| B. | 200名学生的体重是总体的一个样本 | |
| C. | 每名学生是总体的一个个体 | |
| D. | 以上调查是普查 |
10.2014年中国吸引外国投资达1280亿美元,成为全球外国投资第一大目的地国,将1280亿美元用科学记数法表示为( )
| A. | 12.8×1010美元 | B. | 1.28×1011美元 | C. | 1.28×1012美元 | D. | 0.128×1013美元 |
7.比0大的数是( )
| A. | -2 | B. | -$\frac{3}{2}$ | C. | -0.5 | D. | 1 |
11.某市户籍人口1694000人,则该市户籍人口数据用科学记数法可表示为( )
| A. | 1.694×104人 | B. | 1.694×105人 | C. | 1.694×106人 | D. | 1.694×107人 |
8.抛物线y=3x2+2x-1向上平移4个单位长度后的函数解析式为( )
| A. | y=3x2+2x-5 | B. | y=3x2+2x-4 | C. | y=3x2+2x+3 | D. | y=3x2+2x+4 |