题目内容
解方程组 时,一学生把c看错而得到
时,一学生把c看错而得到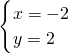 ,而正确的解是
,而正确的解是 ,那么a,b,c的值应是
,那么a,b,c的值应是
- A.不能确定
- B.a=4,b=5,c=-2
- C.a,b不能确定,c=-2
- D.a=4,b=7,c=2
B
分析:虽然看错了c,但题中两组解都符合方程1,代入方程1可得到一个关于a和b的二元一次方程组,用适当的方法解答即可求出a和b.至于c,可把正确结果代入方程2,直接求解.
解答:把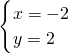 和
和 分别代入ax+by=2,得
分别代入ax+by=2,得
 ,
,
(1)+(2)得:a=4.
代入(1)解得:b=5.
把 代入cx-7y=8得:3c+14=8,
代入cx-7y=8得:3c+14=8,
所以c=-2.
故选B.
点评:本题需要深刻了解二元一次方程及方程组的解的定义以及二元一次方程组的解法.
(1)使二元一次方程两边都相等的两个未知数的值,叫做二元一次方程组的解;
(2)二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
分析:虽然看错了c,但题中两组解都符合方程1,代入方程1可得到一个关于a和b的二元一次方程组,用适当的方法解答即可求出a和b.至于c,可把正确结果代入方程2,直接求解.
解答:把
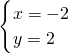 和
和 分别代入ax+by=2,得
分别代入ax+by=2,得 ,
,(1)+(2)得:a=4.
代入(1)解得:b=5.
把
 代入cx-7y=8得:3c+14=8,
代入cx-7y=8得:3c+14=8,所以c=-2.
故选B.
点评:本题需要深刻了解二元一次方程及方程组的解的定义以及二元一次方程组的解法.
(1)使二元一次方程两边都相等的两个未知数的值,叫做二元一次方程组的解;
(2)二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
解方程组 时,一学生把c看错得
时,一学生把c看错得 ,已知方程组的正确解是
,已知方程组的正确解是 ,则a、b、c的值是………………………( )
,则a、b、c的值是………………………( )
 时,一学生把c看错得
时,一学生把c看错得 ,已知方程组的正确解是
,已知方程组的正确解是 ,则a、b、c的值是………………………( )
,则a、b、c的值是………………………( )| A. a、b不能确定,c=-2 | B. a、b、c不能确定 |
| C. a=4,b=7,c=2 | D. a=4,b=5,c="-2" |
解方程组 时,一学生把c看错而得
时,一学生把c看错而得 而正确的解是
而正确的解是 那么 ( )
那么 ( )
 时,一学生把c看错而得
时,一学生把c看错而得 而正确的解是
而正确的解是 那么 ( )
那么 ( )| A.a、b、c的值不能确定 | B.a=4,b=5,c=-2 |
| C.a、b不能确定,c=-2 | D.a=4,b=7,c=2 |
 时,一学生把
时,一学生把 看错而得
看错而得 ,而正确的解是
,而正确的解是 那么
那么 、
、 、
、 时,一学生把c看错而得
时,一学生把c看错而得 而正确的解是
而正确的解是 那么
( )
那么
( )