题目内容
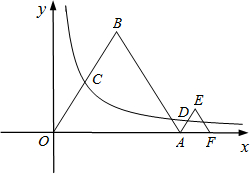
如图(1),直线y=x与双曲线y=
交于点A、C,且OA=OC=
.
(1)求点A的坐标和k的值;
(2)以AC为对角线作矩形ABCD交x轴正半轴于B,交x轴负半轴于D,求点B、D坐标;
(3)如图(2),在(2)的条件下,点B1、D1分别在x轴正、负半轴上移动,AD1交y轴于E,若∠B1AD1=∠BAD,则四边形AB1,OE的面积S是否会发生变化?若不变求S值,若变化求S的 取值范围.
取值范围.
| k |
| x |
| 2 |
(1)求点A的坐标和k的值;
(2)以AC为对角线作矩形ABCD交x轴正半轴于B,交x轴负半轴于D,求点B、D坐标;
(3)如图(2),在(2)的条件下,点B1、D1分别在x轴正、负半轴上移动,AD1交y轴于E,若∠B1AD1=∠BAD,则四边形AB1,OE的面积S是否会发生变化?若不变求S值,若变化求S的
 取值范围.
取值范围.(1)∵点A在直线y=x上,设A(a,a),a>0.作AM⊥x轴于M,
∴OM=AM=a,在Rt△AOM中,由勾股定理,得
OM2+AM2=OA2,
∴a2+a2=(
)2,且a>0,
∴a=1,
∴A(1,1),同理得C(-1,-1).
∵点A在双曲线y=
上,
∴k=1.
(2)∵四边形ABCD是矩形,
∴AO=BO=CO=DO,
∴BO=OD=
.
∵点B在x轴的正半轴,点D在x轴的负半轴,
∴B(
,0),D(-
,0)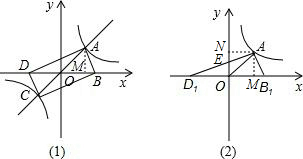
(3)S值不变,为1.
作AM⊥x轴于M,AN⊥y轴于N,
∴AM=AN=1,在矩形ABCD中∠BAD=90°,
∴∠B1AD1=∠BAD=90°,
∵AM⊥x轴于M,AN⊥y轴于N,OM⊥ON,
∴∠MAN=90°,
∴∠B1AM=∠EAN,
∵AM=AN,∠AMB1=∠ANE=90°,
∴△B1AM≌△EAN,
∴S△B1AM=S△EAN,
∴S△B1AM+S四边形AEOM=S△EAN+S四边形AEOM,
∴S四边形ANOM=S四边形AEOB1=AM•AN=1.
∴OM=AM=a,在Rt△AOM中,由勾股定理,得
OM2+AM2=OA2,
∴a2+a2=(
| 2 |
∴a=1,
∴A(1,1),同理得C(-1,-1).
∵点A在双曲线y=
| k |
| x |
∴k=1.
(2)∵四边形ABCD是矩形,
∴AO=BO=CO=DO,
∴BO=OD=
| 2 |
∵点B在x轴的正半轴,点D在x轴的负半轴,
∴B(
| 2 |
| 2 |

(3)S值不变,为1.
作AM⊥x轴于M,AN⊥y轴于N,
∴AM=AN=1,在矩形ABCD中∠BAD=90°,
∴∠B1AD1=∠BAD=90°,
∵AM⊥x轴于M,AN⊥y轴于N,OM⊥ON,
∴∠MAN=90°,
∴∠B1AM=∠EAN,
∵AM=AN,∠AMB1=∠ANE=90°,
∴△B1AM≌△EAN,
∴S△B1AM=S△EAN,
∴S△B1AM+S四边形AEOM=S△EAN+S四边形AEOM,
∴S四边形ANOM=S四边形AEOB1=AM•AN=1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目