题目内容
18.已知:二次函数y=x2+bx+3与x轴交于A,B两点(点A在点B的左侧)与y轴交于点连接CA和CB,S△ABC=3.求b的值.分析 先确定C点坐标为(0,3),再根据三角形面积公式可得AB=2,设A(m,0),B(n,0),则n-m=2,根据抛物线与x轴的交点问题得到m、n为方程x2+bx+3=0的两根,则利用根与系数的关系得到m+m=-b,mn=3,由于(n-m)2=4,则(m+n)2-4mn=4,即b2-4×3=4,然后解关于b的方程即可.
解答 解:当x=0时,y=x2+bx+3=3,则C(0,3),
∵S△ABC=3,
∴$\frac{1}{2}$•AB•3=3,
∴AB=2,
设A(m,0),B(n,0),则n-m=2,
∵m、n为方程x2+bx+3=0的两根,
∴m+m=-b,mn=3,
∵(n-m)2=4,
∴(m+n)2-4mn=4,
∴b2-4×3=4,
∴b=±4.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了根与系数的关系.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
9.当x=3时,(x2-x)-(x2+2x)+1的值等于( )
| A. | 8 | B. | -8 | C. | -6 | D. | 6 |
4.菱形有一个内角为120°,较短对角线为6,则菱形的周长为( )
| A. | 12 | B. | 24 | C. | 36 | D. | 12$\sqrt{3}$ |
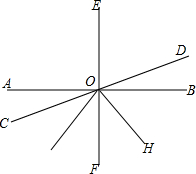 如图,AB、CD、EF相交于点O,EF⊥AB,OG平分∠COF,OH平分∠DOG,若∠AOC:∠DOH=8:29,求∠COH的大小.
如图,AB、CD、EF相交于点O,EF⊥AB,OG平分∠COF,OH平分∠DOG,若∠AOC:∠DOH=8:29,求∠COH的大小. 如图,四边形ABCD中,点E、G、F、H分别是边AD、BC和对角线BD、AC的中点,则四边形EFGH的形状是平行四边形
如图,四边形ABCD中,点E、G、F、H分别是边AD、BC和对角线BD、AC的中点,则四边形EFGH的形状是平行四边形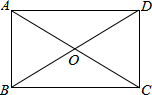 如图,矩形ABCD的两条对角线相交于点O,已知,AB=OA=3cm,求BD与AD的长.
如图,矩形ABCD的两条对角线相交于点O,已知,AB=OA=3cm,求BD与AD的长.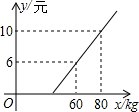 某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票y(元)是行李质量x(kg)的一次函数,其图象如图.求:
某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票y(元)是行李质量x(kg)的一次函数,其图象如图.求: