题目内容
(1)引入:如图1,直线AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC,直线BC是否与⊙O相切,为什么?

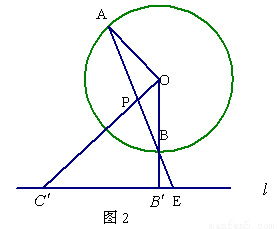
(2)引申:记(1)中⊙O的切线为直线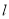 ,在(1)的条件下,如图2,将切线
,在(1)的条件下,如图2,将切线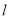 向下平移,设平移后的直线
向下平移,设平移后的直线 与OB的延长线相交于点
与OB的延长线相交于点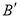 ,与AB的延长线相交于点E,与OP的延长线相交于点
,与AB的延长线相交于点E,与OP的延长线相交于点 .
.
找出图2中与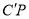 相等的线段,并说明理由;
相等的线段,并说明理由;
如果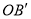 =9cm,
=9cm, =12cm,⊙O的半径为6cm,试求线段
=12cm,⊙O的半径为6cm,试求线段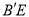 的长.
的长.
(1)相切;理由见解析;(2)① ,理由见解析;②
,理由见解析;② .
.
【解析】
试题分析:(1)根据题意证明OB⊥BC即可;
(2)①根据题意可证明 ,由等角对等边知
,由等角对等边知 ;
;
②设 ,由条件知
,由条件知 ,再利用△AOP∽
,再利用△AOP∽ ,即可求出
,即可求出 的长.
的长.
试题解析:直线BC与⊙O相切
∵OC⊥OA
∴∠A+∠APO=90°
∵OA=OB CB=CP
∴∠A=∠ABO, ∠CPB=∠CBP
∵∠APO=∠CPB
∴∠ABO+∠CBP=90°
即OB⊥BC
又点B在⊙O上
∴直线BC与⊙O相切.
(2)①
∵OA=OB
∴∠OAB=∠OBA
∵
∴
由题意知

∴
∴
∵
∴
∴
∵
∴
∴
设 ,在
,在 中,
中,

则 ,
,

∵ ,
,
∴△AOP∽
∴ 即
即
得
∴
考点:圆的综合题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
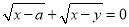 (a>0)
(a>0)
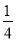 .
.
 中,AB=
中,AB= ,∠B=∠
,∠B=∠ ,补充条件后仍不一定能保证△ABC≌△
,补充条件后仍不一定能保证△ABC≌△ ,则补充的这个条件是( )
,则补充的这个条件是( ) 
 B.∠A=∠
B.∠A=∠ C.AC=
C.AC= D.∠C=∠
D.∠C=∠

