题目内容
在直角坐标系中,抛物线y=x2+mx-| 3 |
| 4 |
| 1 |
| OB |
| 1 |
| OA |
| 2 |
| 3 |
分析:设方程x2+mx-
m2=0的两根分别为x1、x2,由一元二次方程根与系数的关系及m的取值范围判断出x1<0,x2>0,再由
-
=
求出OA=|x1|=-x1,OB=x2,再把OA=|x1|=-x1,OB=x2代入
-
=
即可求出m的值.
| 3 |
| 4 |
| 1 |
| OB |
| 1 |
| OA |
| 2 |
| 3 |
| 1 |
| OB |
| 1 |
| OA |
| 2 |
| 3 |
解答:解:设方程x2+mx-
m2=0的两根分别为x1、x2,且x1<x2,则有x1+x2=-m<0,x1x2=-
m2<0,
所以x1<0,x2>0,由
-
=
,可知OA>OB,又m>0,
所以抛物线的对称轴在y轴的左侧,于是OA=|x1|=-x1,OB=x2,
所以
+
=
,即
=
,
故
=
,
解得m=2.
故答案为:2
| 3 |
| 4 |
| 3 |
| 4 |
所以x1<0,x2>0,由
| 1 |
| OB |
| 1 |
| OA |
| 2 |
| 3 |
所以抛物线的对称轴在y轴的左侧,于是OA=|x1|=-x1,OB=x2,
所以
| 1 |
| x1 |
| 1 |
| x2 |
| 2 |
| 3 |
| x1+x2 |
| x1x2 |
| 2 |
| 3 |
故
| -m | ||
-
|
| 2 |
| 3 |
解得m=2.
故答案为:2
点评:本题考查的是抛物线与x轴的交点及一元二次方程根与系数的关系,根据已知条件求出OA=|x1|=-x1,OB=x2是解答此题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
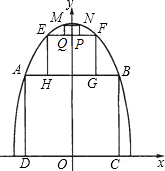 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求: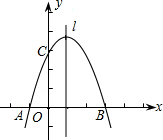 ,B,C三点的抛物的对称轴为直线l,D为对称轴l上一动点.
,B,C三点的抛物的对称轴为直线l,D为对称轴l上一动点.
 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求: (2005•杭州)为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
(2005•杭州)为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求: