题目内容
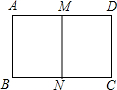如图，把矩形ABCD对折，折痕为MN，矩形DMNC与矩形ABCD相似，已知AB=4．
（1）求AD的长；
（2）求矩形DMNC与矩形ABCD的相似比．
解：（1）由已知得MN=AB，MD=
AD=BC，
∵矩形DMNC与矩形ABCD相似，
，
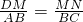∵MN=AB，DM=AD，BC=AD，
∴AD2=AB2，
∴由AB=4得，AD=4
；
（2）矩形DMNC与矩形ABCD的相似比为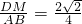
=
．
分析：（1）矩形DMNC与矩形ABCD相似，对应边的比相等，就可以得到AD的长；
（2）相似比即为是对应边的比．
点评：本题考查相似多边形的性质，对应边的比相等．
AD=BC，∵矩形DMNC与矩形ABCD相似，
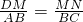，∵MN=AB，DM=
AD，BC=AD，∴
AD2=AB2，∴由AB=4得，AD=4
；（2）矩形DMNC与矩形ABCD的相似比为
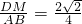=．分析：（1）矩形DMNC与矩形ABCD相似，对应边的比相等，就可以得到AD的长；
（2）相似比即为是对应边的比．
点评：本题考查相似多边形的性质，对应边的比相等．
练习册系列答案
备战中考寒假系列答案
相关题目
如图，把矩形ABCD沿直线EF折叠，使点C与A重合．
24、如图，把矩形ABCD沿对角线BD对折，使点C落在点C′处，试证明AE=C′E．
（2013•梧州）如图，把矩形ABCD沿直线EF折叠，若∠1=20°，则∠2=（ ）
如图，把矩形ABCD沿EF折叠，使点A与点C重叠．AB=8，BC=16，求DF的长．
如图，把矩形ABCD沿EF折叠，若∠1=50°，则∠AEF等于