题目内容
3.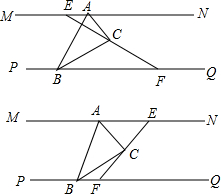 如图,MN∥PQ,∠NAB和∠QBA的平分线相交于点C,点E是直线MN上一个可移动点(不与点A重合),射线EC与PQ相交于点F.
如图,MN∥PQ,∠NAB和∠QBA的平分线相交于点C,点E是直线MN上一个可移动点(不与点A重合),射线EC与PQ相交于点F.(1)∠ACB=90°,证明:AE+AB=BF;
(2)当点E移动到点A的右侧时,上述结论是怎样的?画出图形,直接写出.
分析 (1)作辅助线,构建全等三角形,先根据平行线的性质和角平分线得出:∠BAC+∠ABC=90°,再根据等角对等边得AB=AD,利用三线合一得AC=CD,从而证明△AEC≌△DFC,得AE=DF,代入可得结论;
(2)结论不成立,有新的结论存在:AB=BF+AE,同理得:AB=BD,△ACE≌△DCF,有BD=BF+DF,
等量代换可得:AB=BF+AE.
解答 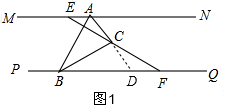 (1)证明:如图1,∵MN∥PQ,
(1)证明:如图1,∵MN∥PQ,
∴∠NAB+∠ABF=180°,
∵∠NAB和∠QBA的平分线相交于点C,
∴∠BAC=$\frac{1}{2}$∠NAB,∠ABC=$\frac{1}{2}$∠ABF,
∴∠BAC+∠ABC=$\frac{1}{2}$(∠NAB+∠ABF)=$\frac{1}{2}$×180°=90°,
延长AC交PQ于D,
∵MN∥PQ,
∴∠NAD=∠ADB,
∵∠NAD=∠BAC,
∴∠BAC=∠ADB,
∴AB=AD,
∴AC=CD,
∵∠ACE=∠DCF,∠EAC=∠FDC,
∴△AEC≌△DFC,
∴AE=DF,
∴BF=BD+DF=AB+AE;
故答案为:90;
(2)如图2,有AB=BF+AE,理由是: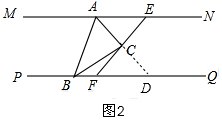
延长AC交PQ于D,
由(1)得:AB=BD,
∴AC=CD,
∵∠EAC=∠ADF,∠ACE=∠DCF,
∴△ACE≌△DCF,
∴AE=DF,
∵BD=BF+DF,
∴AB=BF+AE.
点评 本题考查了全等三角形的性质和判定,以及角平分线、平行线的性质;明确两直线平行,同旁内角互补,注意角平分线平分角时有三种表达方式,在证明中恰当地写出适合本题的一种:∠BAC=$\frac{1}{2}$∠NAB,恰当地构建辅助线也是本题的关键;两个问题中的结论虽然不同,但证明思路一致:①先由平行和角平分线定义得直角△ACB,②证明等腰△ABD,利用三线合一得AC=CD,③证明三角形全等.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案 已知:如图,在△ABC中,AB=AC,点D,E,F分别在边BC,BA,CA上,且BE=CD,BD=CF.求证:点D在线段EF的垂直平分线上.
已知:如图,在△ABC中,AB=AC,点D,E,F分别在边BC,BA,CA上,且BE=CD,BD=CF.求证:点D在线段EF的垂直平分线上.
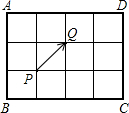 如图是一个小型的台球桌,四角分别是A,B,C,D四个球筐,桌面可以分成12个正方形小区域,如果将在点P位置的球沿着PQ的方向击球Q,那么球Q最终会落在( )
如图是一个小型的台球桌,四角分别是A,B,C,D四个球筐,桌面可以分成12个正方形小区域,如果将在点P位置的球沿着PQ的方向击球Q,那么球Q最终会落在( )