题目内容
6.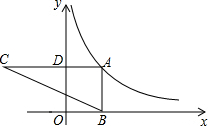 如图,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使AD=DC,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为4,则反比例函数的解析式为( )
如图,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使AD=DC,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为4,则反比例函数的解析式为( )| A. | y=$\frac{2}{x}$ | B. | y=$\frac{3}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=$\frac{5}{x}$ |
分析 连结BD,利用三角形面积公式得到S△ADB=$\frac{1}{2}$S△BAC=2,则S矩形OBAD=2S△ADB=4,于是可根据反比例函数的比例系数k的几何意义得到k的值.
解答  解:连结BD,如图,
解:连结BD,如图,
∵AD=DC,
∴S△ADB=S△BDC=$\frac{1}{2}$S△BAC=$\frac{1}{2}$×4=2,
∵AD⊥y轴于点D,AB⊥x轴,
∴四边形OBAD为矩形,
∴S矩形OBAD=2S△ADB=2×2=4,
∴k=4.
∴反比例函数的解析式为y=$\frac{4}{x}$,
故选C.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
1.一个数的平方是正数,则这个数是( )
| A. | 正数 | B. | 负数 | C. | 不为零的数 | D. | 非负数 |
11.有一组数据:2,5,7,2,3,3,6,下列结论错误的是( )
| A. | 中位数为3 | B. | 众数为2 | C. | 平均数为4 | D. | 极差是5 |