题目内容
 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B,C.若矩形ABOC的面积为6,求点A坐标.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B,C.若矩形ABOC的面积为6,求点A坐标.考点:一次函数图象上点的坐标特征
专题:计算题
分析:根据一次函数图象上点的坐标特征,可设A点坐标为(t,-2t+8)(0<t<4),再利用矩形ABOC的面积为6得到t(-2t+8)=6,解得t1=1,t2=3,然后分别计算出自变量为1和3的函数值即可得到A点坐标.
解答:解:当y=0时,-2x+8=0,解得x=4,则P点坐标为(4,0)
设A点坐标为(t,-2t+8)(0<t<4),则AB=-2t+8,OB=t,
根据题意得t(-2t+8)=6,
整理得t2-4t+3=0,解得t1=1,t2=3,
当t=1时,-2t+8=6;
当t=3时,-2t+8=2,
所以点A的坐标为(1,6)或(3,2).
设A点坐标为(t,-2t+8)(0<t<4),则AB=-2t+8,OB=t,
根据题意得t(-2t+8)=6,
整理得t2-4t+3=0,解得t1=1,t2=3,
当t=1时,-2t+8=6;
当t=3时,-2t+8=2,
所以点A的坐标为(1,6)或(3,2).
点评:本题考查了一次函数图象上点的坐标特征:一次函数图象上点的坐标满足其解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,那么下列结论正确的是( )
如图,那么下列结论正确的是( )| A、a比b大 |
| B、b比a大 |
| C、a、b一样大 |
| D、a、b的大小无法确定 |
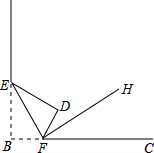 如图,将长方形纸片的一角斜折过去,使点B落在点D处,EF为折痕,再把FC折过去与FD重合,FH为折痕,问:
如图,将长方形纸片的一角斜折过去,使点B落在点D处,EF为折痕,再把FC折过去与FD重合,FH为折痕,问: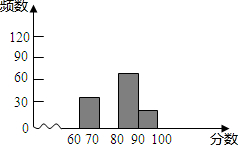 为迎接国庆,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:
为迎接国庆,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表如下: 如图,已知矩形ABCD的边AB=1,BC=3,现把矩形ABCD绕着它的对称中心旋转,若重叠部分的形状为菱形且面积为S,则S的取值范围为
如图,已知矩形ABCD的边AB=1,BC=3,现把矩形ABCD绕着它的对称中心旋转,若重叠部分的形状为菱形且面积为S,则S的取值范围为 已知二次函数y=x2+bx+c的图象如图所示,它与x轴的一个交点的坐标为A(-1,0),与y轴的交点的坐标为C(0,-3).
已知二次函数y=x2+bx+c的图象如图所示,它与x轴的一个交点的坐标为A(-1,0),与y轴的交点的坐标为C(0,-3).